20×20 array this number is larger than the total number of particles in the universe. So it seems quite inconceivable that systems in nature could ever carry out such an exhaustive search.
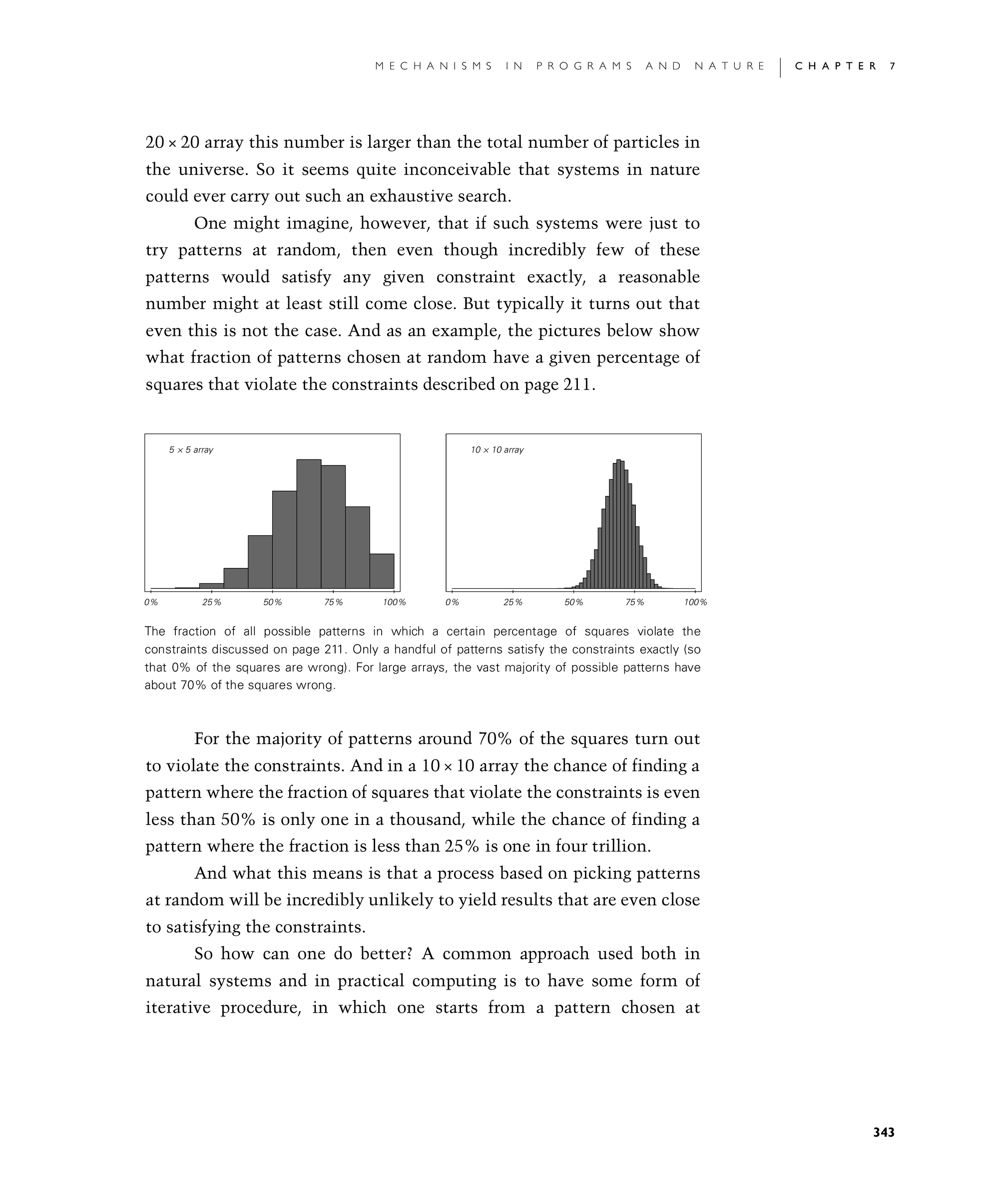
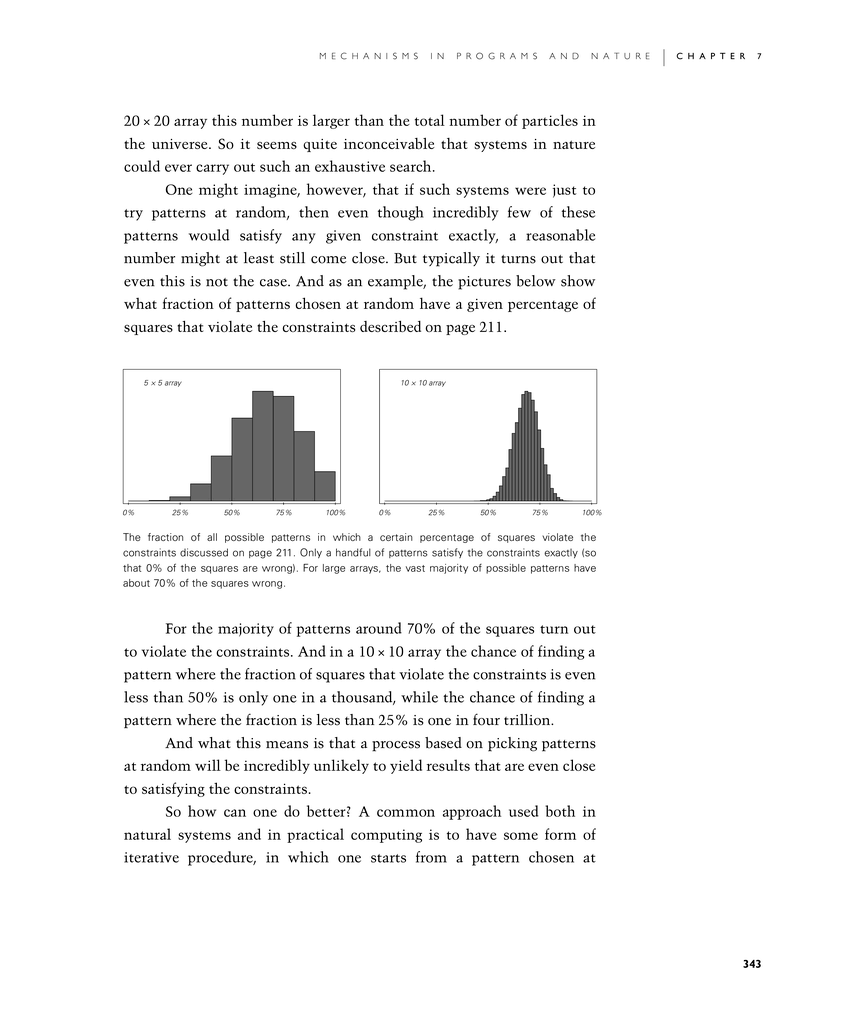
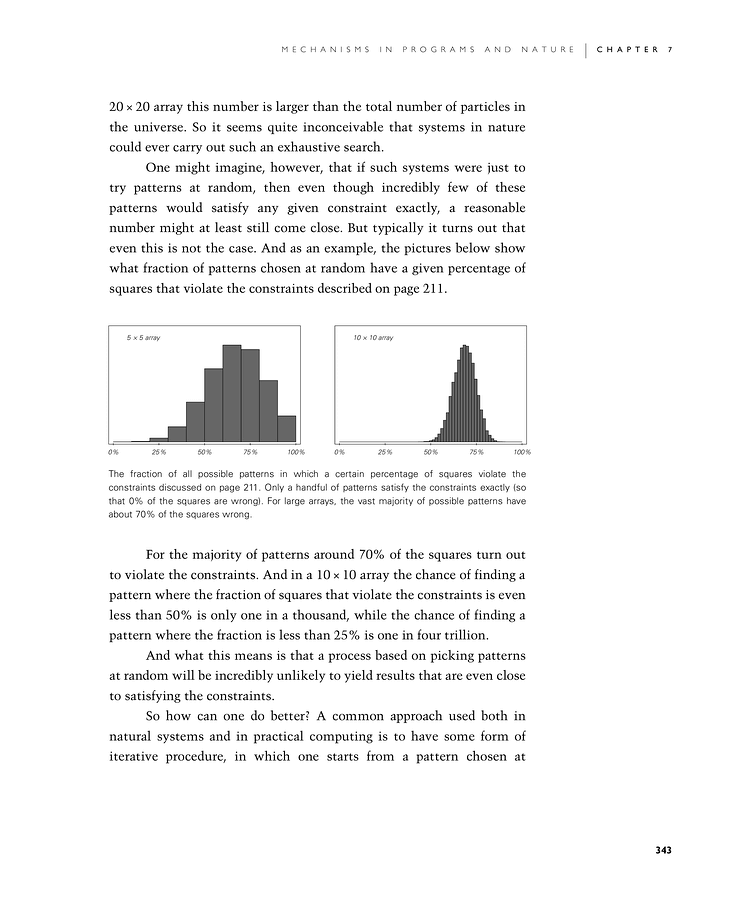
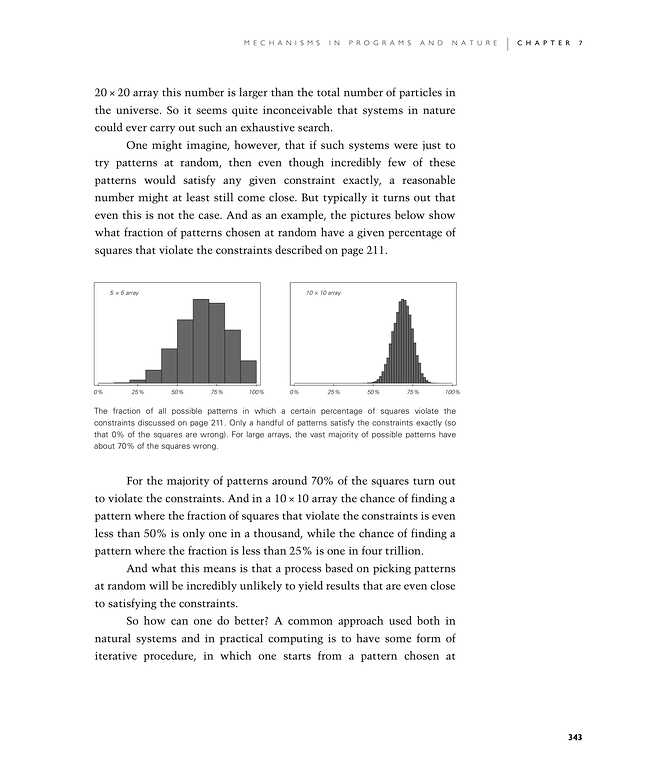
One might imagine, however, that if such systems were just to try patterns at random, then even though incredibly few of these patterns would satisfy any given constraint exactly, a reasonable number might at least still come close. But typically it turns out that even this is not the case. And as an example, the pictures below show what fraction of patterns chosen at random have a given percentage of squares that violate the constraints described on page 211.
For the majority of patterns around 70% of the squares turn out to violate the constraints. And in a 10×10 array the chance of finding a pattern where the fraction of squares that violate the constraints is even less than 50% is only one in a thousand, while the chance of finding a pattern where the fraction is less than 25% is one in four trillion.
And what this means is that a process based on picking patterns at random will be incredibly unlikely to yield results that are even close to satisfying the constraints.
So how can one do better? A common approach used both in natural systems and in practical computing is to have some form of iterative procedure, in which one starts from a pattern chosen at

The fraction of all possible patterns in which a certain percentage of squares violate the constraints discussed on page 211. Only a handful of patterns satisfy the constraints exactly (so that 0% of the squares are wrong). For large arrays, the vast majority of possible patterns have about 70% of the squares wrong.