Substitution Systems and Fractals
One-dimensional substitution systems of the kind we discussed on page 82 can be thought of as working by progressively subdividing each element they contain into several smaller elements.
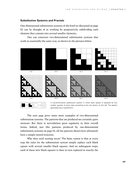
One can construct two-dimensional substitution systems that work in essentially the same way, as shown in the pictures below.
The next page gives some more examples of two-dimensional substitution systems. The patterns that are produced are certainly quite intricate. But there is nevertheless great regularity in their overall forms. Indeed, just like patterns produced by one-dimensional substitution systems on page 83, all the patterns shown here ultimately have a simple nested structure.
Why does such nesting occur? The basic reason is that at every step the rules for the substitution system simply replace each black square with several smaller black squares. And on subsequent steps, each of these new black squares is then in turn replaced in exactly the
A two-dimensional substitution system in which each square is replaced by four smaller squares at every step according to the rule shown on the left. The pattern generated has a nested form.