Mathematical Constants
The last few sections [2, 3, 4] have shown that one can set up all sorts of systems based on numbers in which great complexity can occur. But it turns out that the possibility of such complexity is already suggested by some well-known facts in elementary mathematics.
The facts in question concern the sequences of digits in numbers like π (pi). To a very rough approximation, π is 3.14. A more accurate approximation is 3.14159265358979323846264338327950288.
But how does this sequence of digits continue?
One might suppose that at some level it must be quite simple and regular. For the value of π is specified by the simple definition of being the ratio of the circumference of any circle to its diameter.
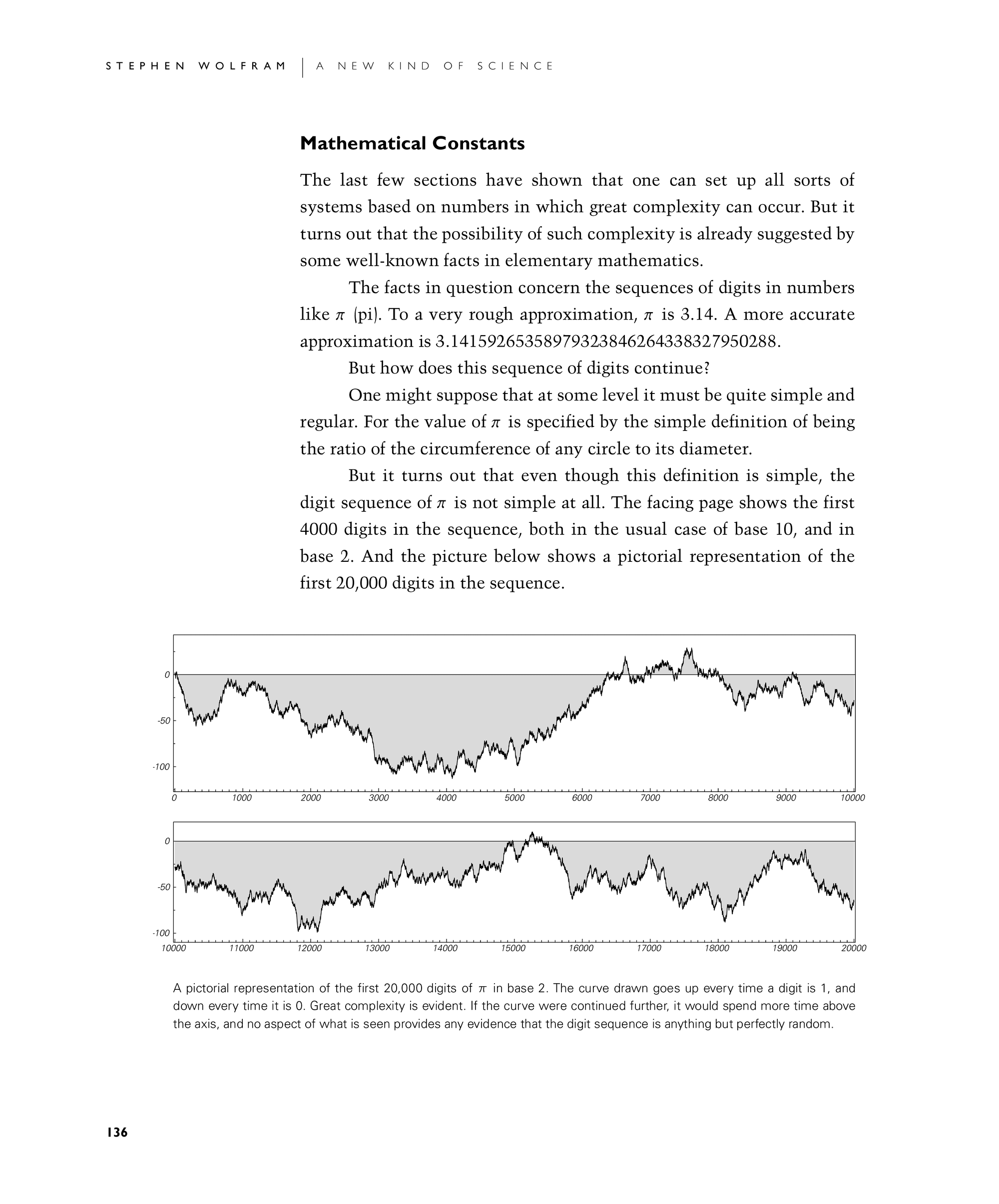
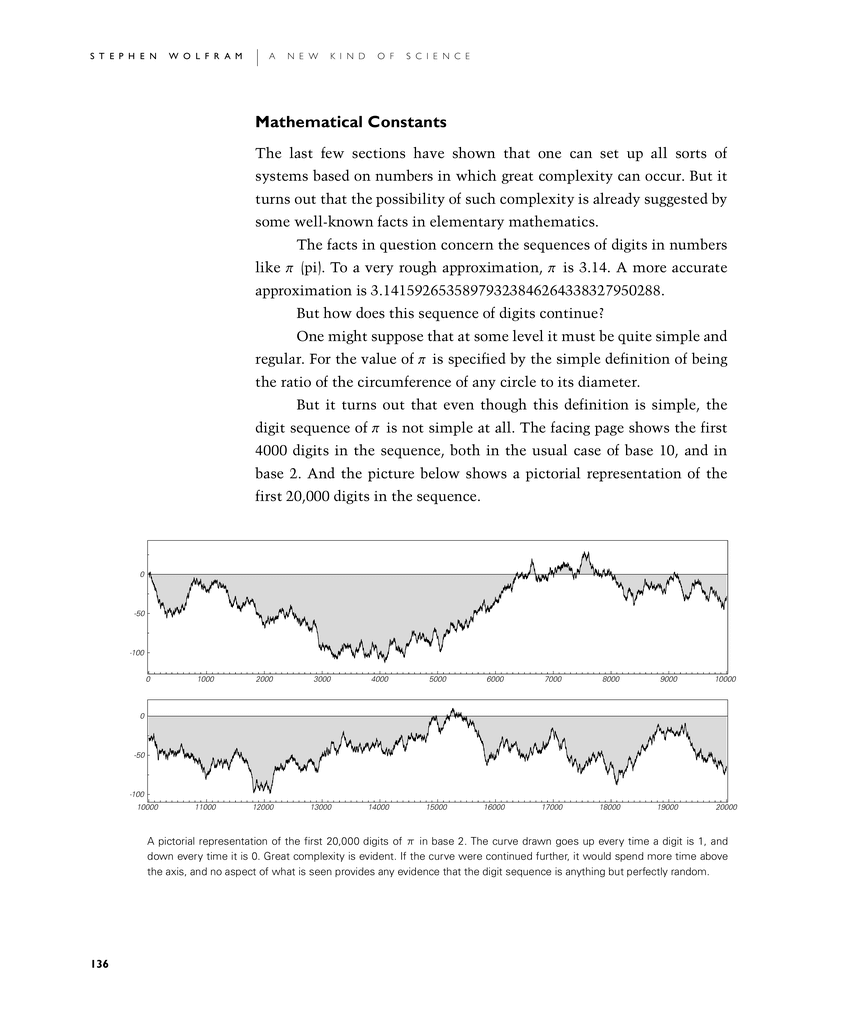
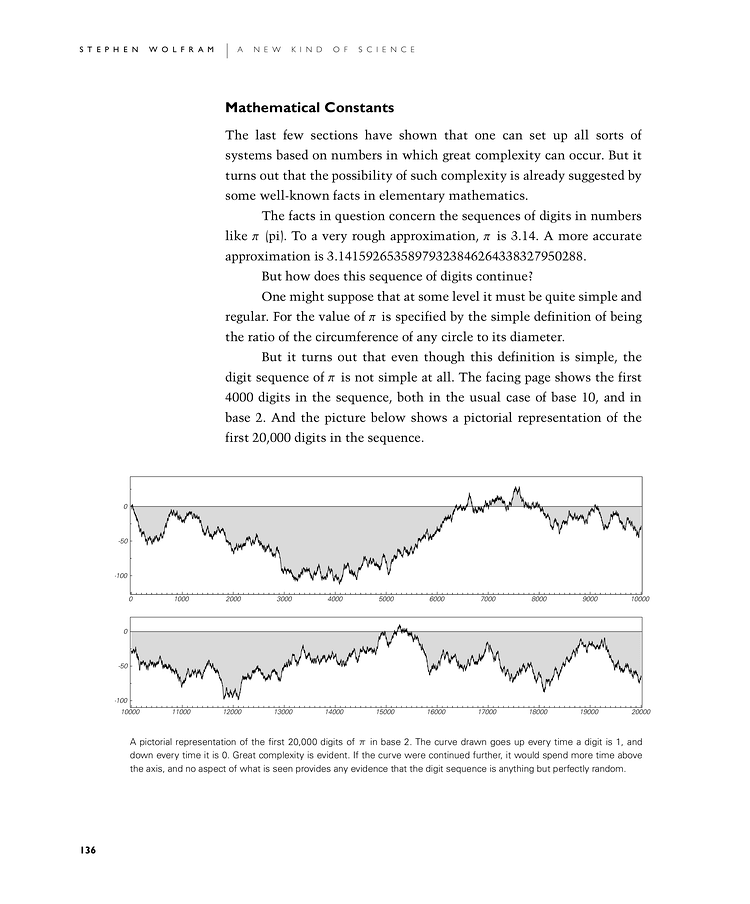
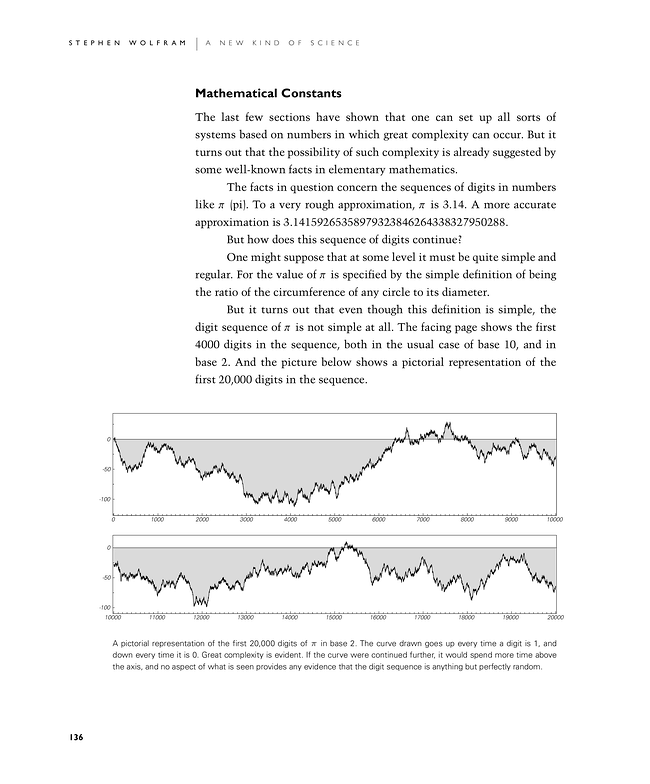
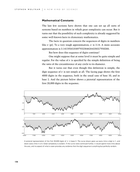
But it turns out that even though this definition is simple, the digit sequence of π is not simple at all. The facing page shows the first 4000 digits in the sequence, both in the usual case of base 10, and in base 2. And the picture below shows a pictorial representation of the first 20,000 digits in the sequence.
A pictorial representation of the first 20,000 digits of π in base 2. The curve drawn goes up every time a digit is 1, and down every time it is 0. Great complexity is evident. If the curve were continued further, it would spend more time above the axis, and no aspect of what is seen provides any evidence that the digit sequence is anything but perfectly random.