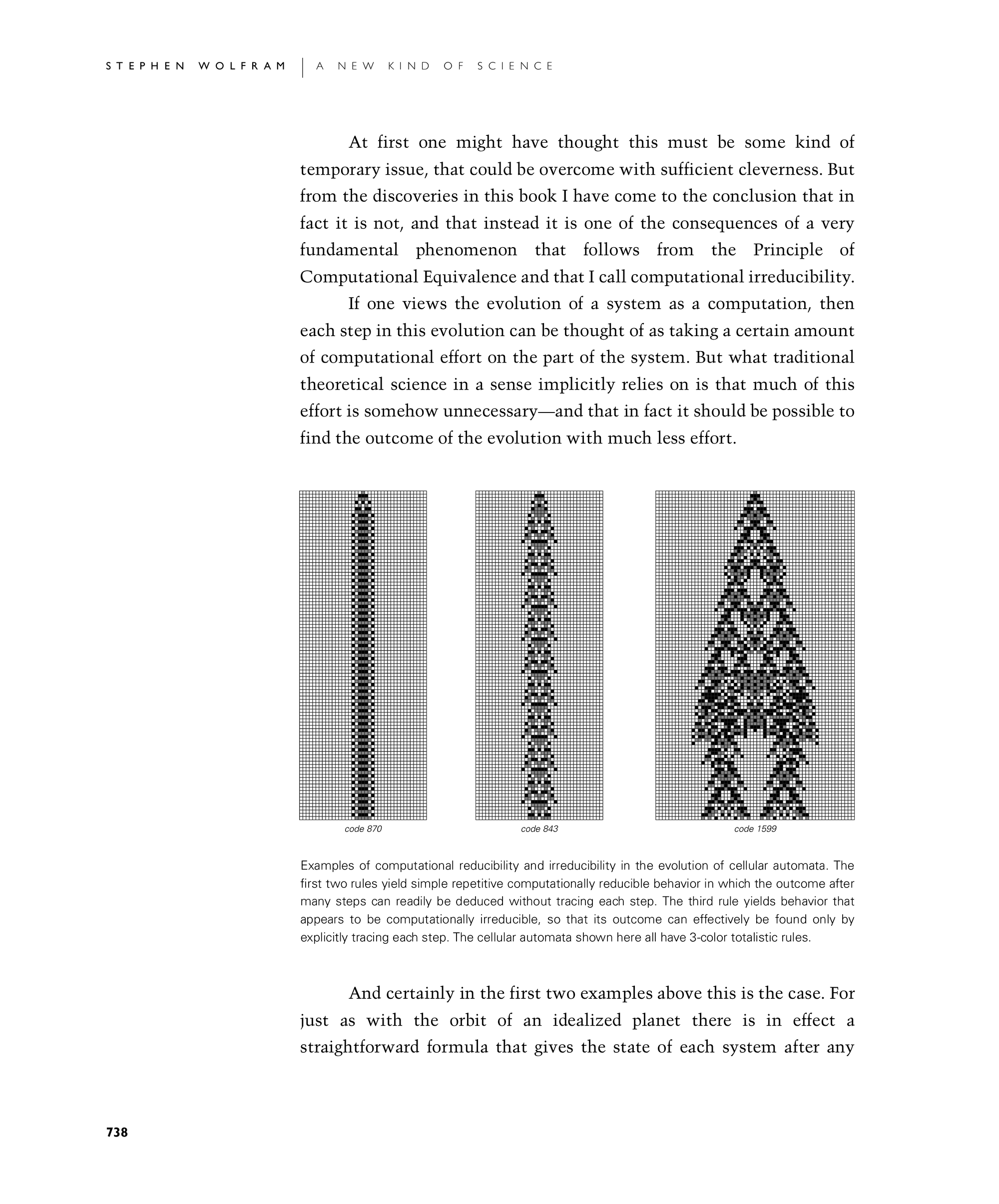
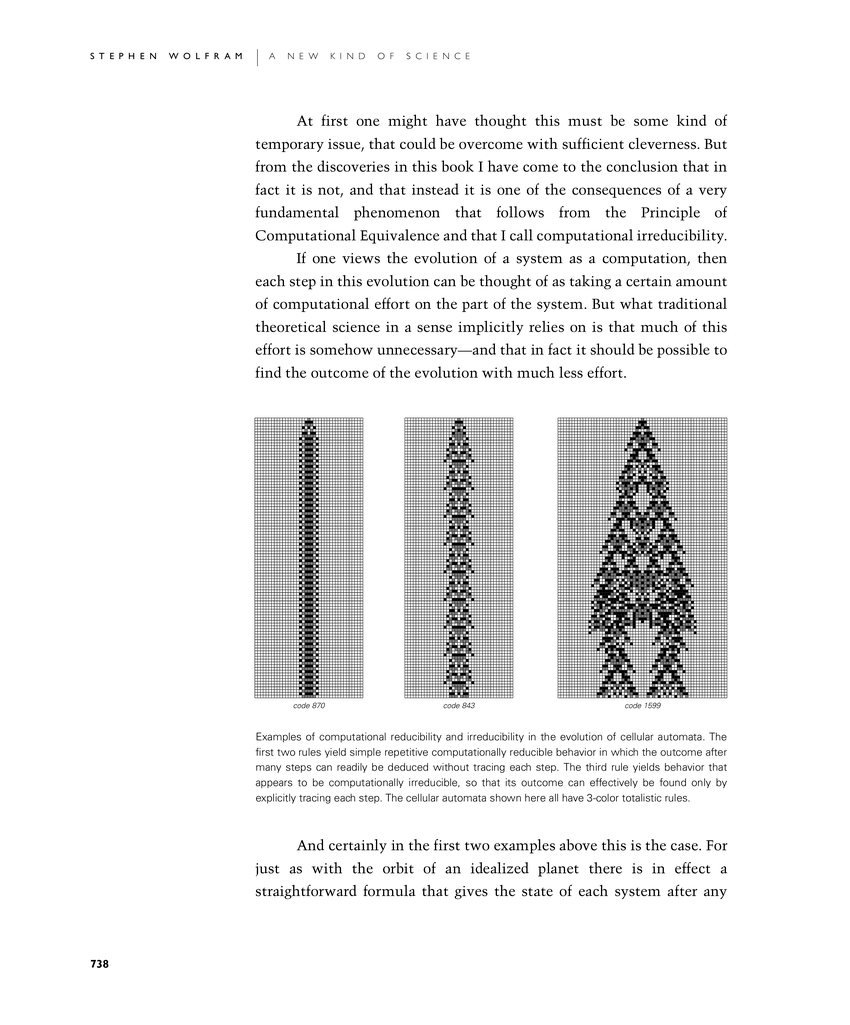
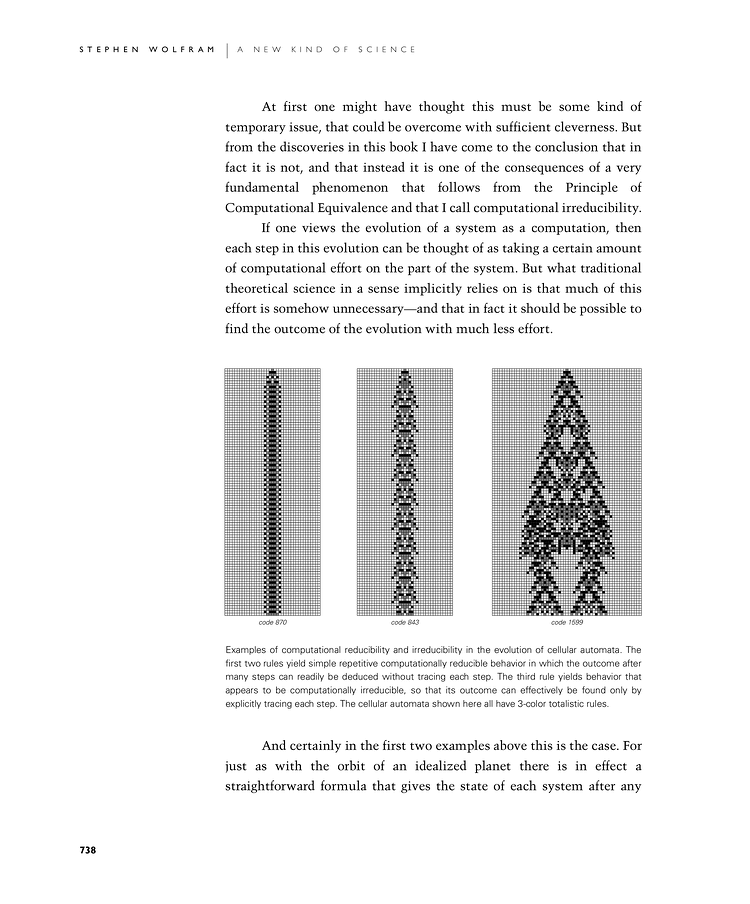
At first one might have thought this must be some kind of temporary issue, that could be overcome with sufficient cleverness. But from the discoveries in this book I have come to the conclusion that in fact it is not, and that instead it is one of the consequences of a very fundamental phenomenon that follows from the Principle of Computational Equivalence and that I call computational irreducibility.
If one views the evolution of a system as a computation, then each step in this evolution can be thought of as taking a certain amount of computational effort on the part of the system. But what traditional theoretical science in a sense implicitly relies on is that much of this effort is somehow unnecessary—and that in fact it should be possible to find the outcome of the evolution with much less effort.
And certainly in the first two examples below this is the case. For just as with the orbit of an idealized planet there is in effect a straightforward formula that gives the state of each system after any

Examples of computational reducibility and irreducibility in the evolution of cellular automata. The first two rules yield simple repetitive computationally reducible behavior in which the outcome after many steps can readily be deduced without tracing each step. The third rule yields behavior that appears to be computationally irreducible, so that its outcome can effectively be found only by explicitly tracing each step. The cellular automata shown here all have 3-color totalistic rules.