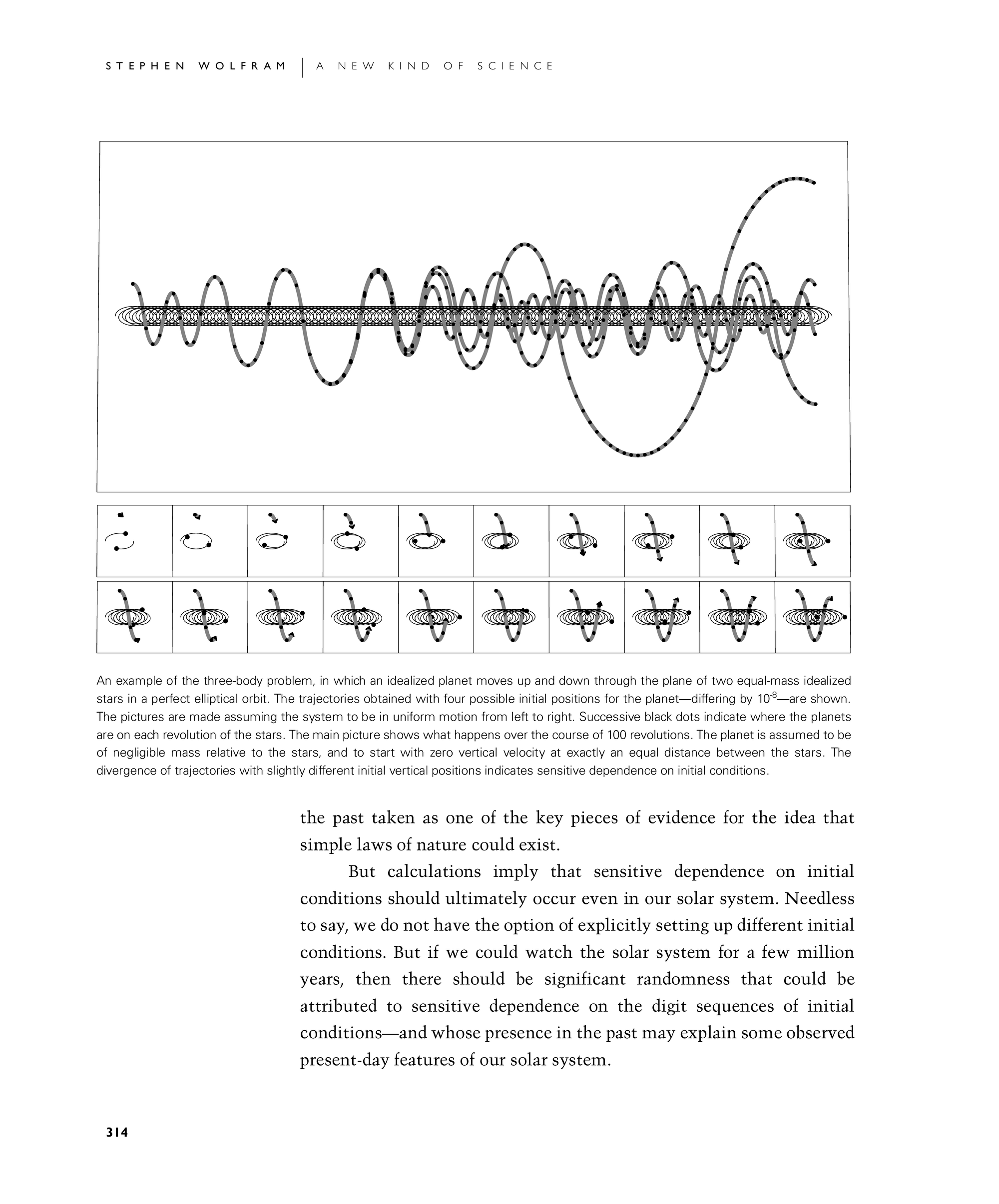
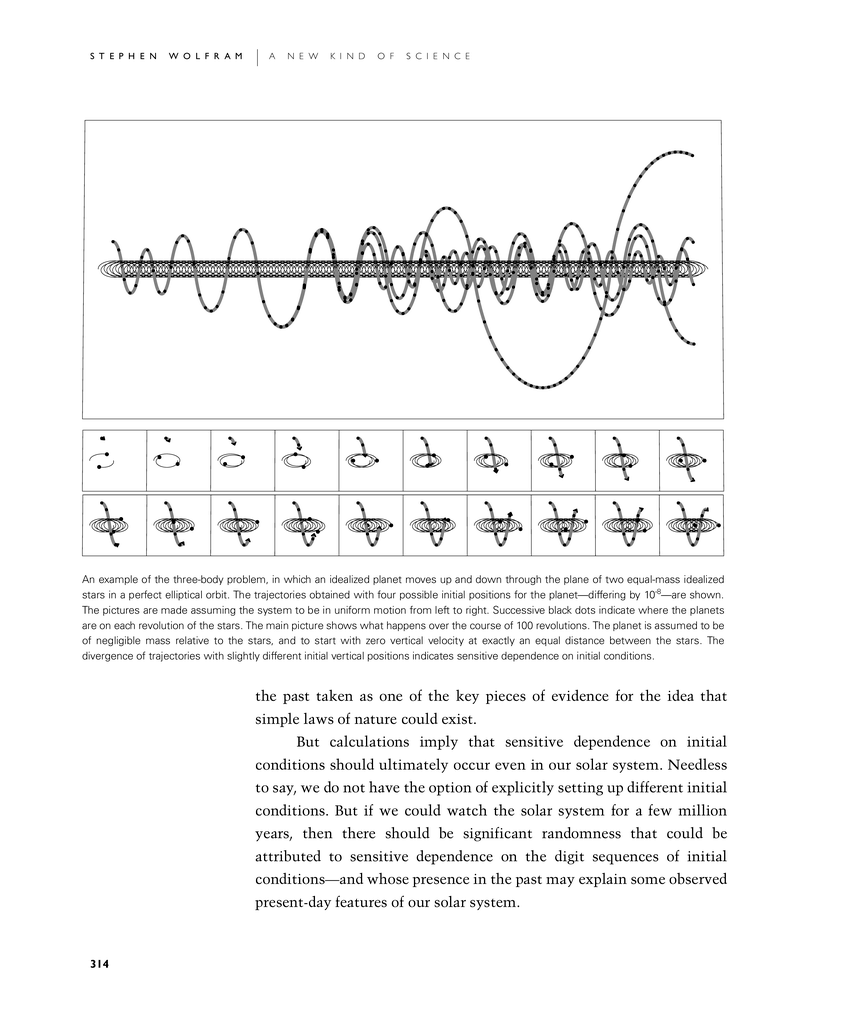
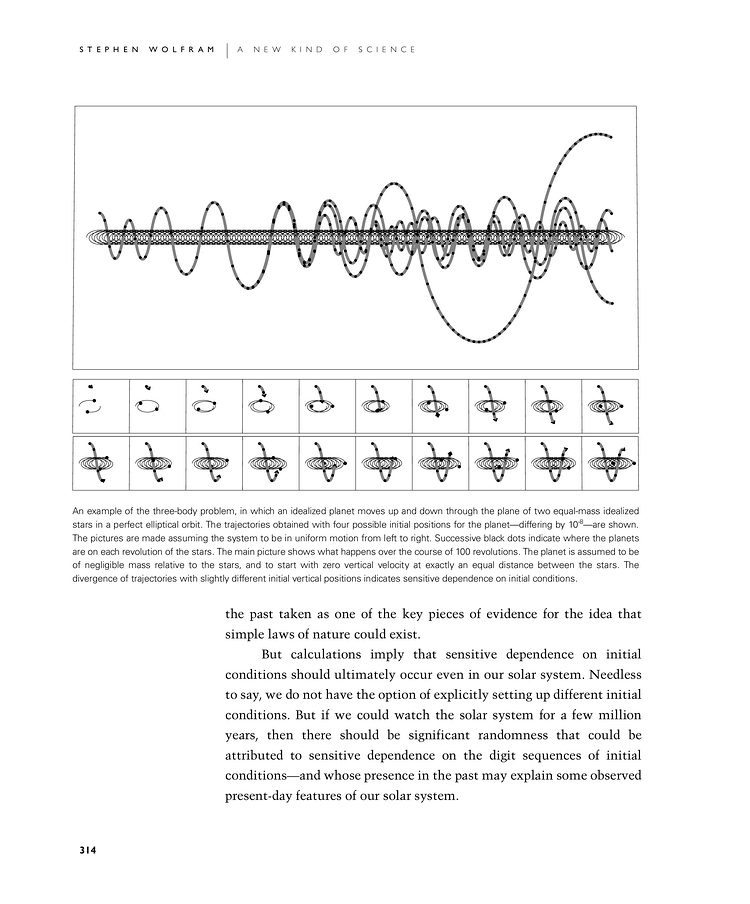
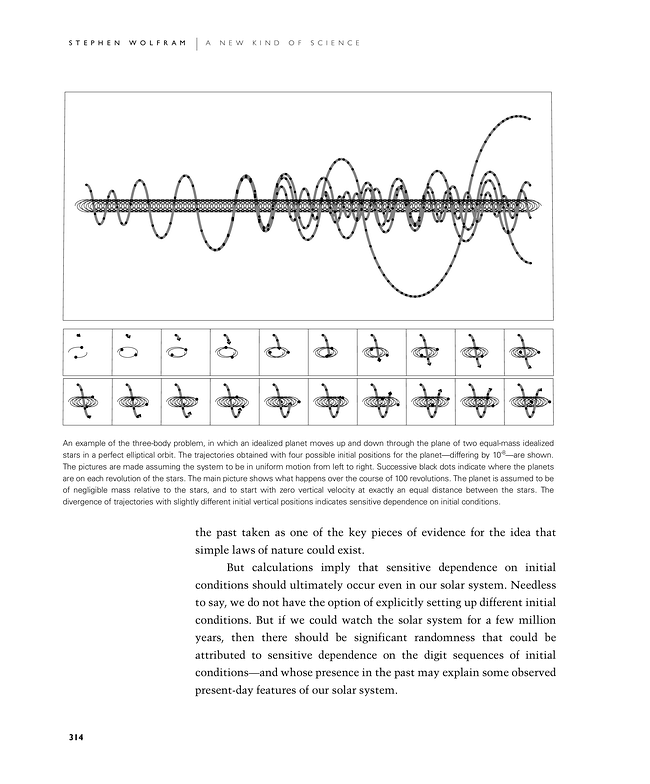
the past taken as one of the key pieces of evidence for the idea that simple laws of nature could exist.

But calculations imply that sensitive dependence on initial conditions should ultimately occur even in our solar system. Needless to say, we do not have the option of explicitly setting up different initial conditions. But if we could watch the solar system for a few million years, then there should be significant randomness that could be attributed to sensitive dependence on the digit sequences of initial conditions—and whose presence in the past may explain some observed present-day features of our solar system.

An example of the three-body problem, in which an idealized planet moves up and down through the plane of two equal-mass idealized stars in a perfect elliptical orbit. The trajectories obtained with four possible initial positions for the planet—differing by 10^-8—are shown. The pictures are made assuming the system to be in uniform motion from left to right. Successive black dots indicate where the planets are on each revolution of the stars. The main picture shows what happens over the course of 100 revolutions. The planet is assumed to be of negligible mass relative to the stars, and to start with zero vertical velocity at exactly an equal distance between the stars. The divergence of trajectories with slightly different initial vertical positions indicates sensitive dependence on initial conditions.