perturbations in the mirrors and by other phenomena that are not accounted for in the simple description we have given.

At the heart of the system shown on the previous page is a slightly complicated arrangement of parabolic mirrors. But it turns out that almost any convex reflector will lead to the divergence of trajectories necessary to get sensitive dependence on initial conditions.

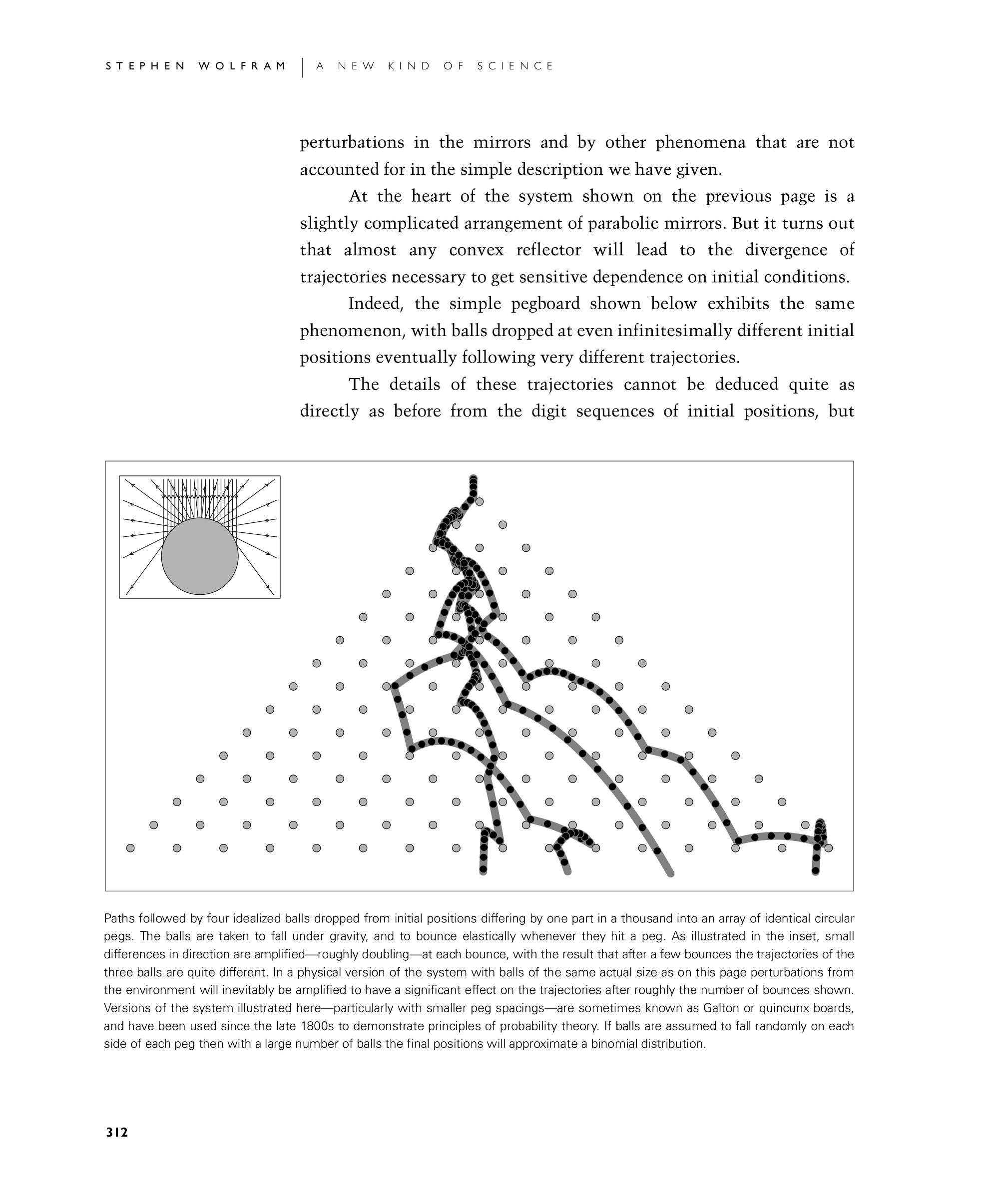
Indeed, the simple pegboard shown below exhibits the same phenomenon, with balls dropped at even infinitesimally different initial positions eventually following very different trajectories.

The details of these trajectories cannot be deduced quite as directly as before from the digit sequences of initial positions, but

Paths followed by four idealized balls dropped from initial positions differing by one part in a thousand into an array of identical circular pegs. The balls are taken to fall under gravity, and to bounce elastically whenever they hit a peg. As illustrated in the inset, small differences in direction are amplified—roughly doubling—at each bounce, with the result that after a few bounces the trajectories of the three balls are quite different. In a physical version of the system with balls of the same actual size as on this page perturbations from the environment will inevitably be amplified to have a significant effect on the trajectories after roughly the number of bounces shown. Versions of the system illustrated here—particularly with smaller peg spacings—are sometimes known as Galton or quincunx boards, and have been used since the late 1800s to demonstrate principles of probability theory. If balls are assumed to fall randomly on each side of each peg then with a large number of balls the final positions will approximate a binomial distribution.