by considering digit sequences in which each digit can again have only a discrete set of possible values, typically just 0 and 1.

So now a question that arises is whether all the complexity we have seen in the past three chapters [2, 3, 4] somehow depends on the discreteness of the elements in the systems we have looked at.

And to address this question, what I will do in this section is to consider a generalization of cellular automata in which each cell is not just black or white, but instead can have any of a continuous range of possible levels of gray. One can update the gray level of each cell by using rules that are in a sense a cross between the totalistic cellular automaton rules that we discussed at the beginning of the last chapter and the iterated maps that we just discussed in the previous section.

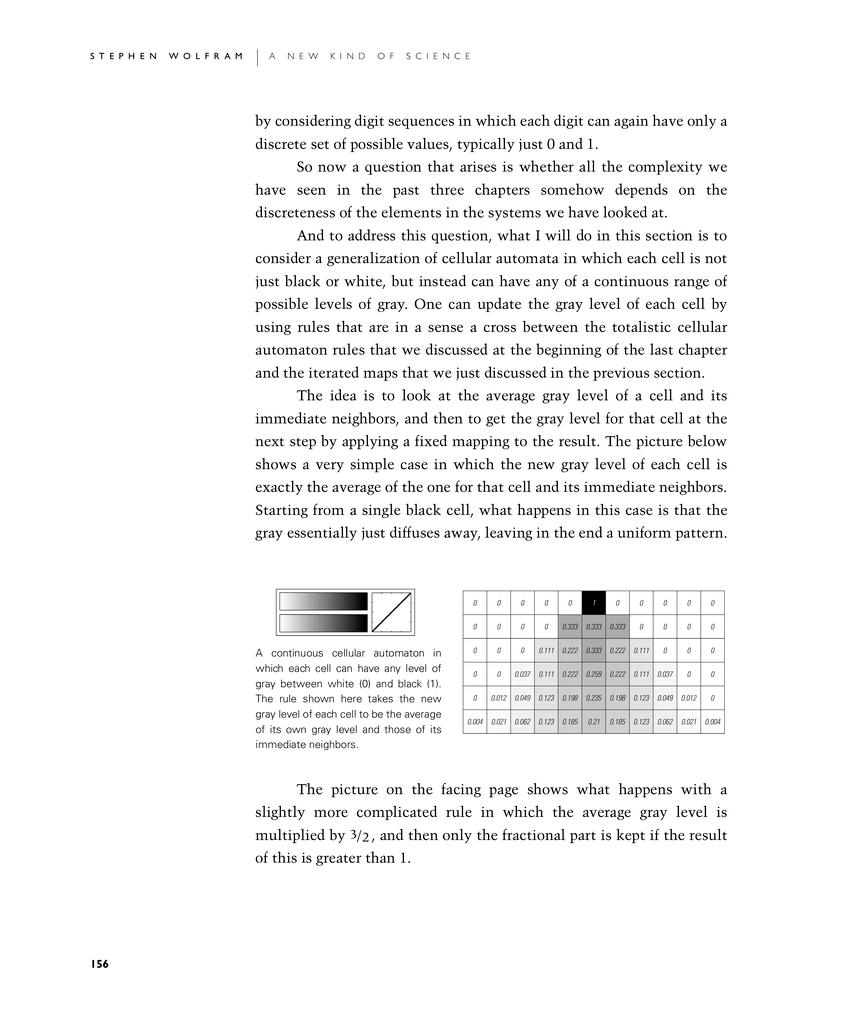
The idea is to look at the average gray level of a cell and its immediate neighbors, and then to get the gray level for that cell at the next step by applying a fixed mapping to the result. The picture below shows a very simple case in which the new gray level of each cell is exactly the average of the one for that cell and its immediate neighbors. Starting from a single black cell, what happens in this case is that the gray essentially just diffuses away, leaving in the end a uniform pattern.

The picture on the facing page shows what happens with a slightly more complicated rule in which the average gray level is multiplied by 3/2, and then only the fractional part is kept if the result of this is greater than 1.

A continuous cellular automaton in which each cell can have any level of gray between white (0) and black (1). The rule shown here takes the new gray level of each cell to be the average of its own gray level and those of its immediate neighbors.