Tag Systems

One of the goals of this chapter is to find out just how simple the underlying structure of a system can be while the system as a whole is still capable of producing complex behavior. And as one example of a class of systems with a particularly simple underlying structure, I consider here what are sometimes known as tag systems.

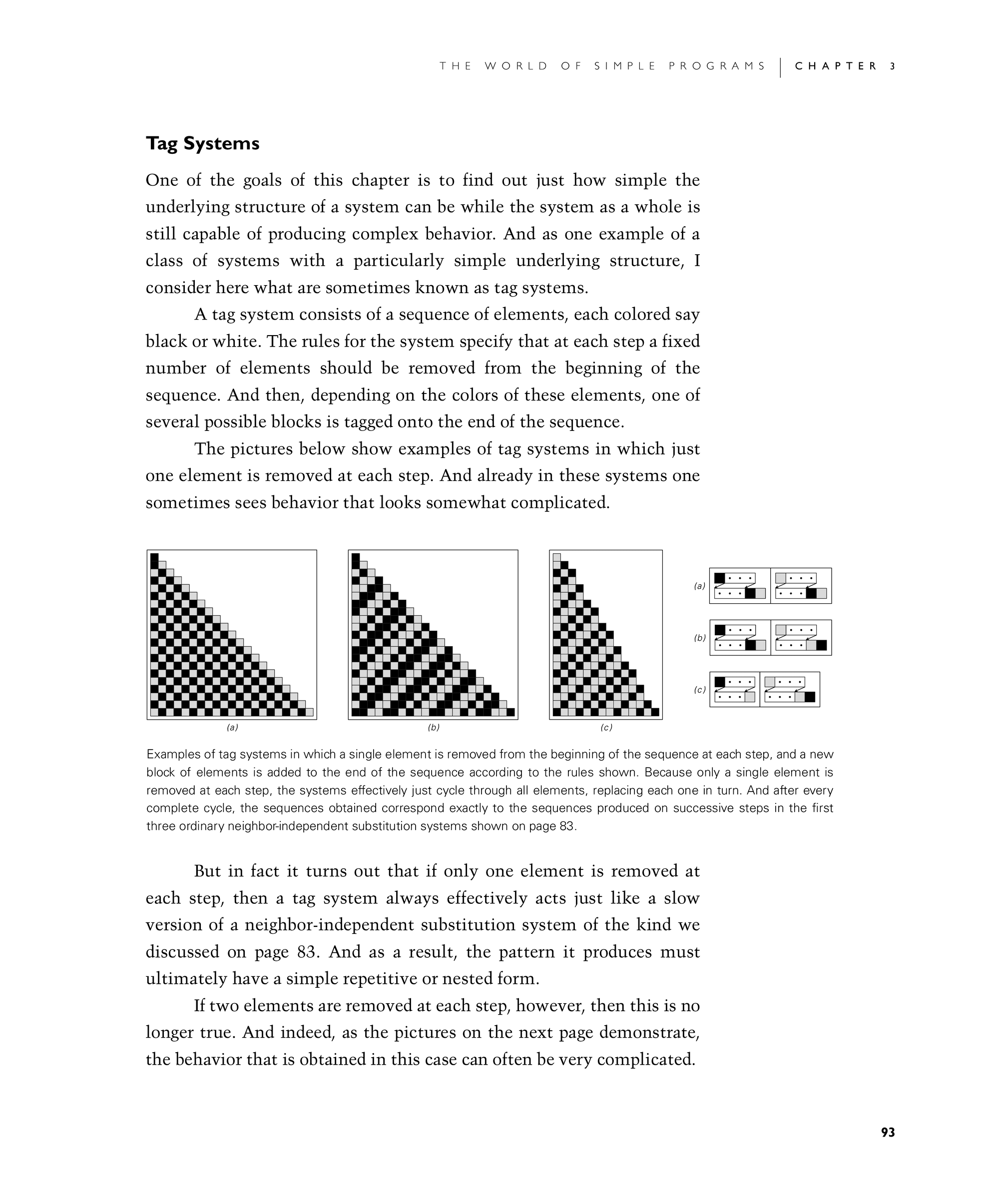
A tag system consists of a sequence of elements, each colored say black or white. The rules for the system specify that at each step a fixed number of elements should be removed from the beginning of the sequence. And then, depending on the colors of these elements, one of several possible blocks is tagged onto the end of the sequence.

The pictures below show examples of tag systems in which just one element is removed at each step. And already in these systems one sometimes sees behavior that looks somewhat complicated.

But in fact it turns out that if only one element is removed at each step, then a tag system always effectively acts just like a slow version of a neighbor-independent substitution system of the kind we discussed on page 83. And as a result, the pattern it produces must ultimately have a simple repetitive or nested form.

If two elements are removed at each step, however, then this is no longer true. And indeed, as the pictures on the next page demonstrate, the behavior that is obtained in this case can often be very complicated.

Examples of tag systems in which a single element is removed from the beginning of the sequence at each step, and a new block of elements is added to the end of the sequence according to the rules shown. Because only a single element is removed at each step, the systems effectively just cycle through all elements, replacing each one in turn. And after every complete cycle, the sequences obtained correspond exactly to the sequences produced on successive steps in the first three ordinary neighbor-independent substitution systems shown on page 83.