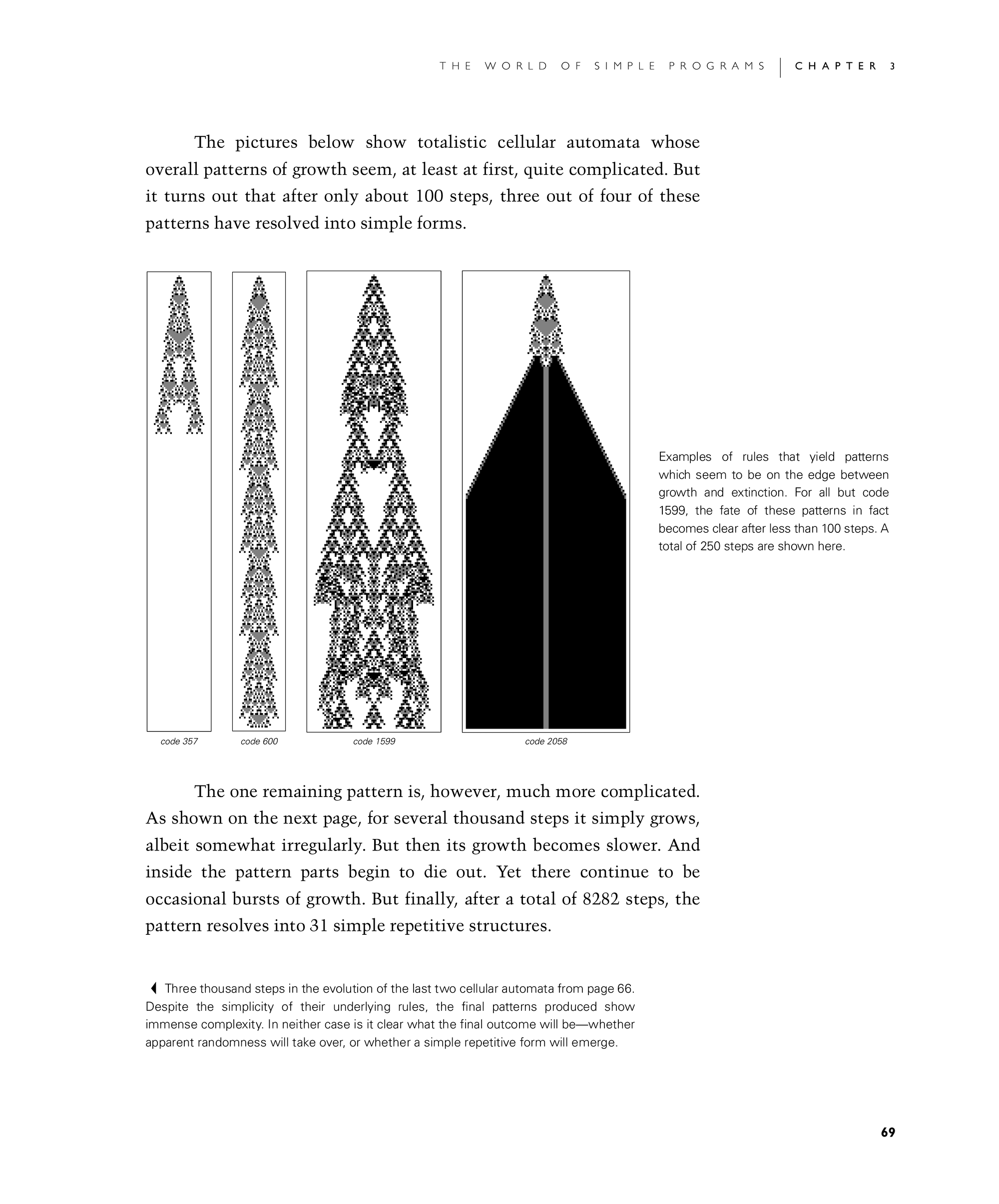
The pictures below show totalistic cellular automata whose overall patterns of growth seem, at least at first, quite complicated. But it turns out that after only about 100 steps, three out of four of these patterns have resolved into simple forms.

The one remaining pattern is, however, much more complicated. As shown on the next page, for several thousand steps it simply grows, albeit somewhat irregularly. But then its growth becomes slower. And inside the pattern parts begin to die out. Yet there continue to be occasional bursts of growth. But finally, after a total of 8282 steps, the pattern resolves into 31 simple repetitive structures.

Examples of rules that yield patterns which seem to be on the edge between growth and extinction. For all but code 1599, the fate of these patterns in fact becomes clear after less than 100 steps. A total of 250 steps are shown here.