But what about random initial conditions? Repetition in time is still easy to achieve—say just by different parts of a system behaving independently. But repetition in space is slightly more difficult to achieve. For even if localized domains of repetition form, they need to have some mechanism for combining together.

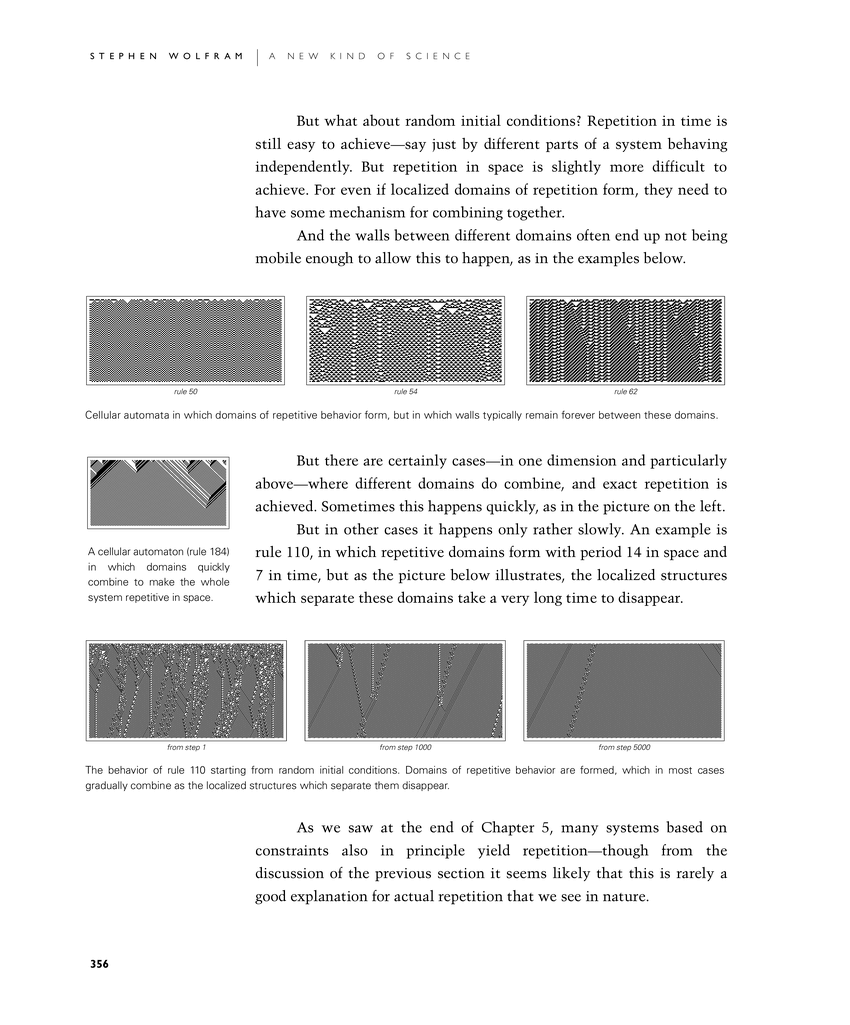
And the walls between different domains often end up not being mobile enough to allow this to happen, as in the first set of examples below.

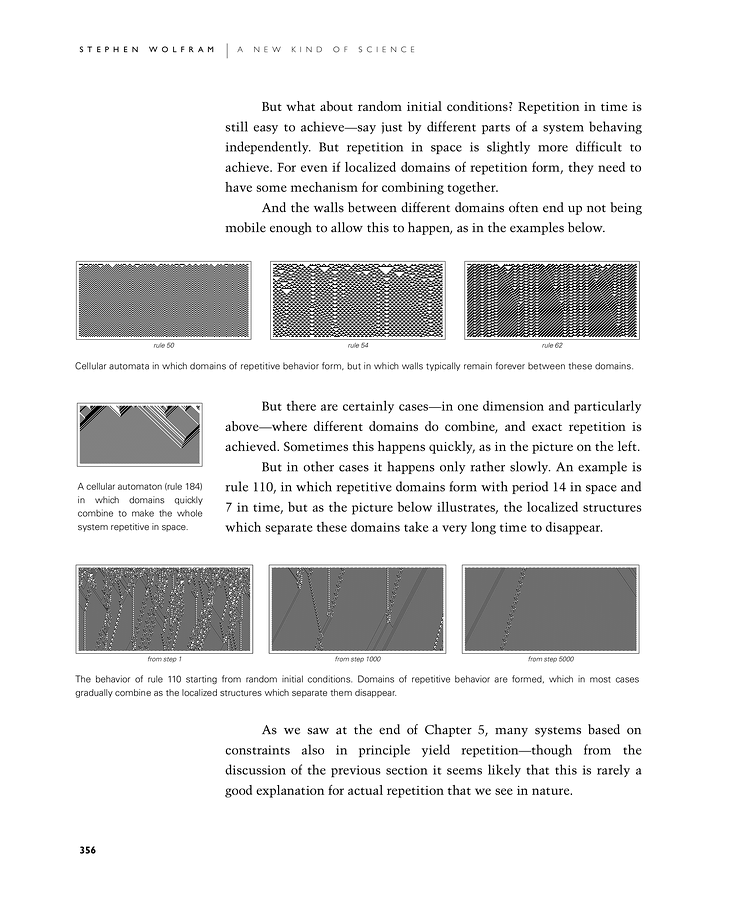
But there are certainly cases—in one dimension and particularly in the first set of images below—where different domains do combine, and exact repetition is achieved. Sometimes this happens quickly, as in the picture on the left.

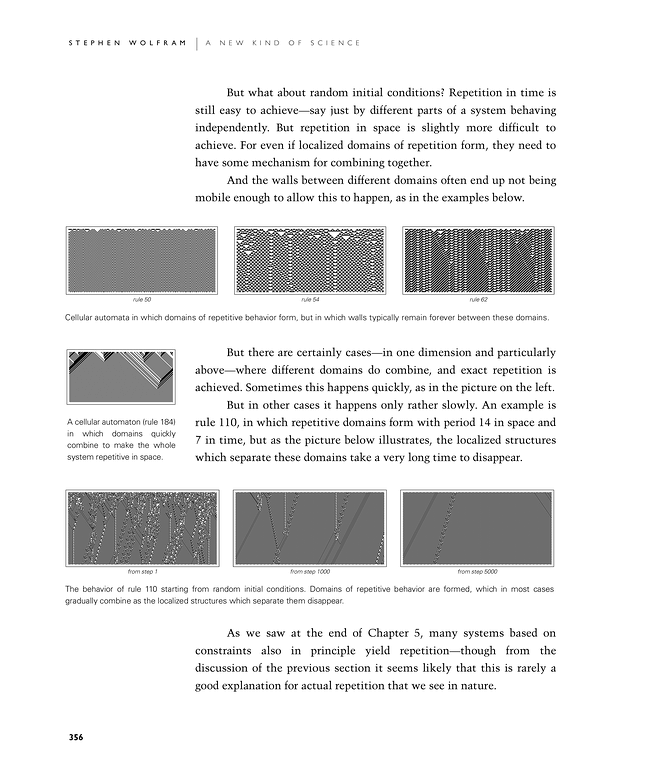
But in other cases it happens only rather slowly. An example is rule 110, in which repetitive domains form with period 14 in space and 7 in time, but as the second picture below illustrates, the localized structures which separate these domains take a very long time to disappear.

As we saw at the end of Chapter 5, many systems based on constraints also in principle yield repetition—though from the discussion of the previous section it seems likely that this is rarely a good explanation for actual repetition that we see in nature.

Cellular automata in which domains of repetitive behavior form, but in which walls typically remain forever between these domains.

A cellular automaton (rule 184) in which domains quickly combine to make the whole system repetitive in space.

The behavior of rule 110 starting from random initial conditions. Domains of repetitive behavior are formed, which in most cases gradually combine as the localized structures which separate them disappear.