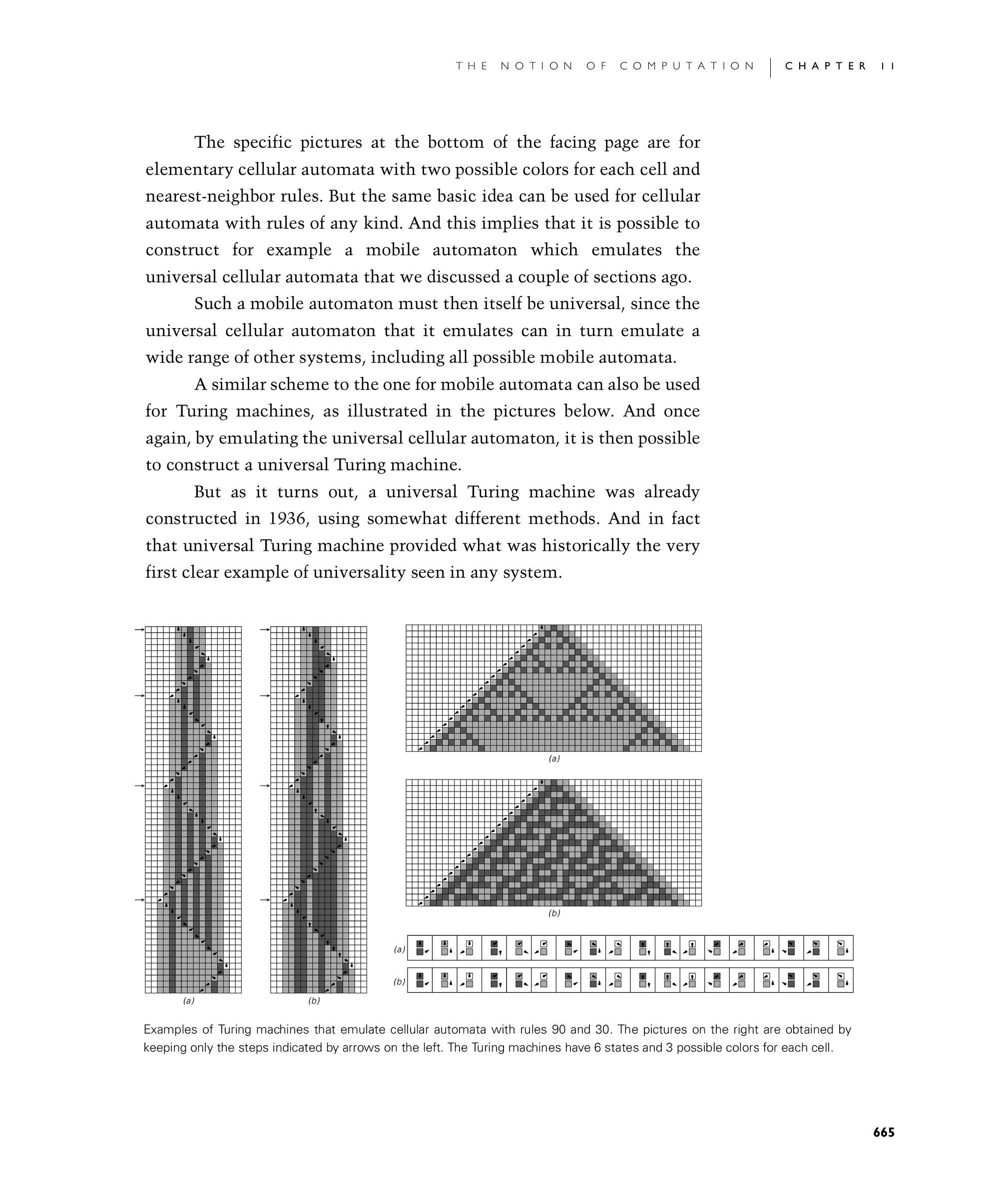
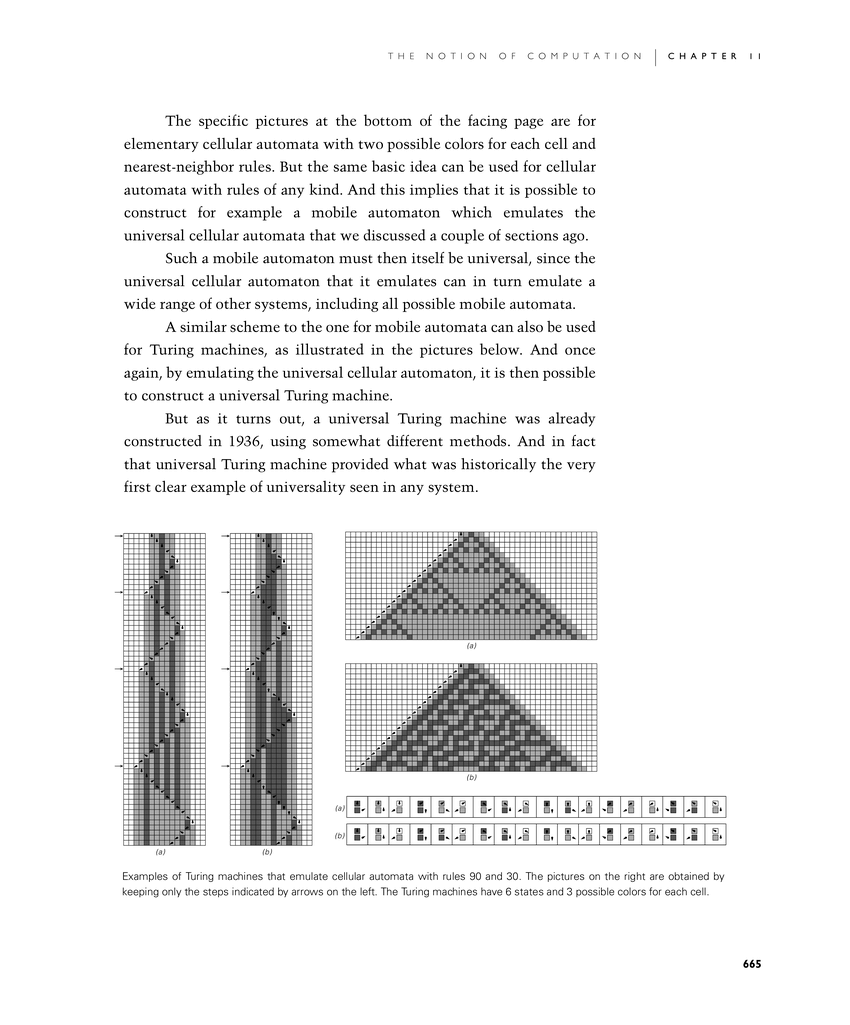
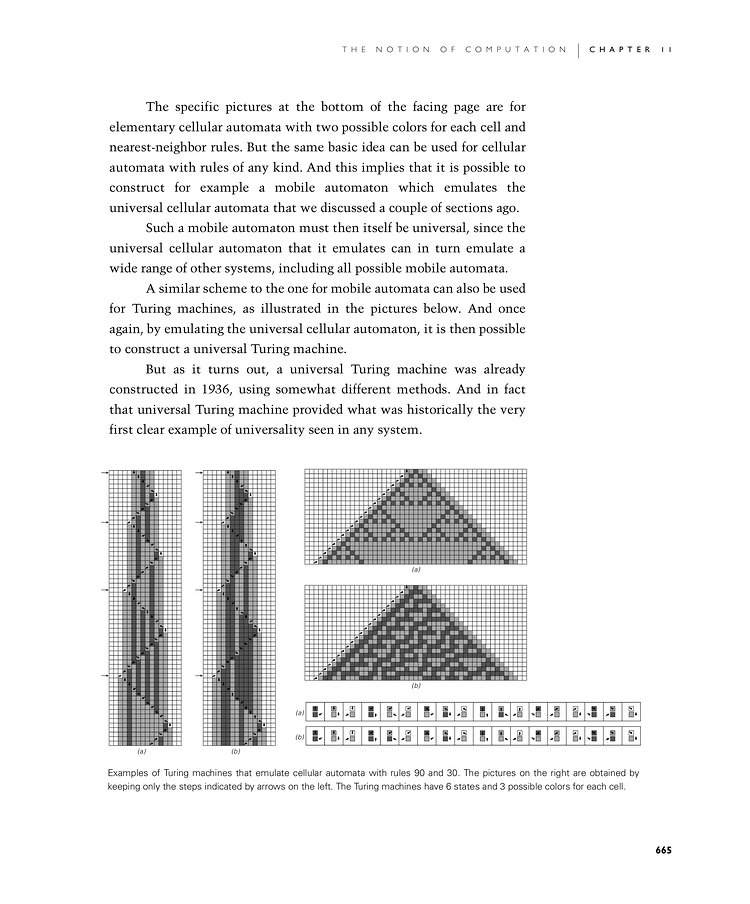
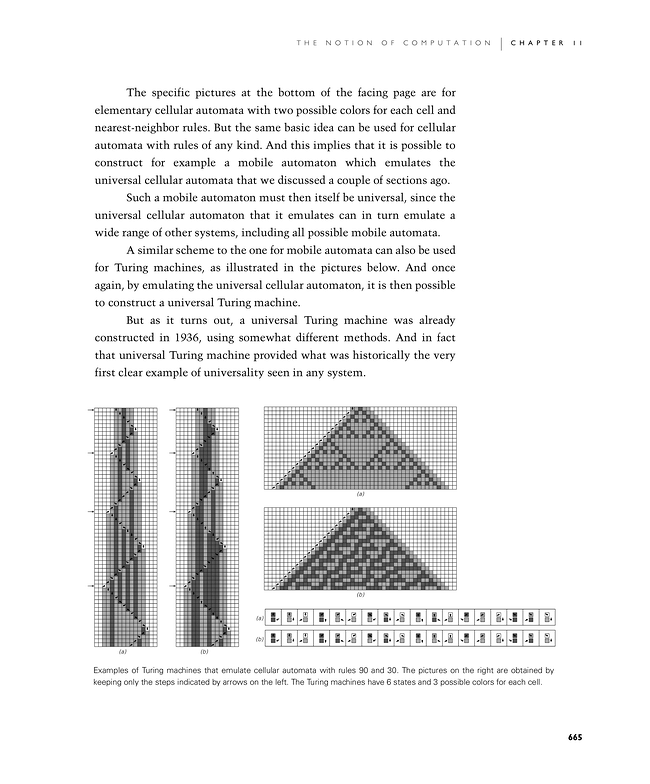
The specific pictures at the bottom of the facing page are for elementary cellular automata with two possible colors for each cell and nearest-neighbor rules. But the same basic idea can be used for cellular automata with rules of any kind. And this implies that it is possible to construct for example a mobile automaton which emulates the universal cellular automata that we discussed a couple of sections ago.

Such a mobile automaton must then itself be universal, since the universal cellular automaton that it emulates can in turn emulate a wide range of other systems, including all possible mobile automata.

A similar scheme to the one for mobile automata can also be used for Turing machines, as illustrated in the pictures below. And once again, by emulating the universal cellular automaton, it is then possible to construct a universal Turing machine.

But as it turns out, a universal Turing machine was already constructed in 1936, using somewhat different methods. And in fact that universal Turing machine provided what was historically the very first clear example of universality seen in any system.

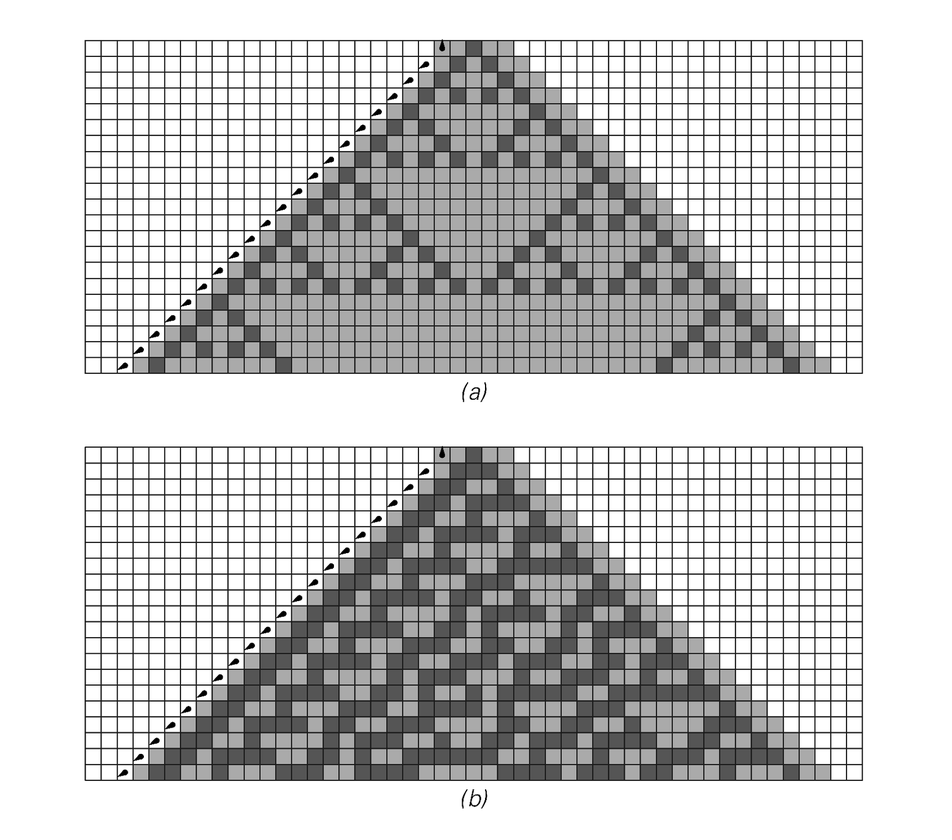Examples of Turing machines that emulate cellular automata with rules 90 and 30. The pictures on the right are obtained by keeping only the steps indicated by arrows on the left. The Turing machines have 6 states and 3 possible colors for each cell.