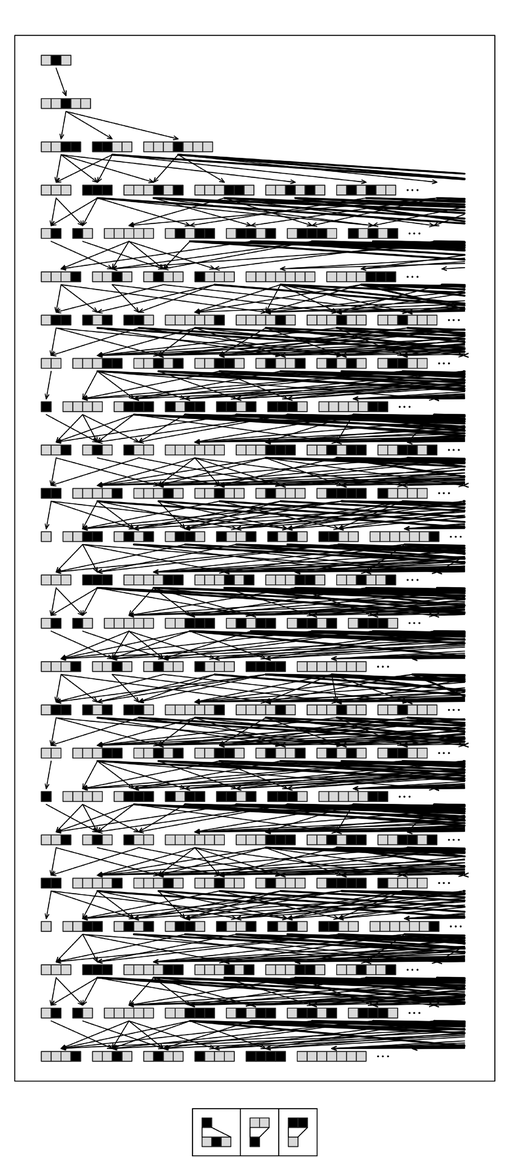
Three examples of multiway systems that show the analog of long proofs. In each case a string consisting of a single white element is eventually generated—but this takes respectively 12, 28 and 34 steps to happen. The first multiway system actually generates all strings in the end (not least since it yields the lemmas -> and ->)—and in fact strings of length n > 2 appear after at most 2n+7 steps. The second multiway system generates only the n+1 strings where black comes before white—and all of these strings appear after at most 7n steps. The third multiway system generates a complicated collection of strings; the numbers of lengths up to 8 are 1, 2, 4, 8, 14, 22, 34, 45. All the strings generated have an even number of black elements.