whatever sequence of digits are left behind being taken to be the output of the computation.

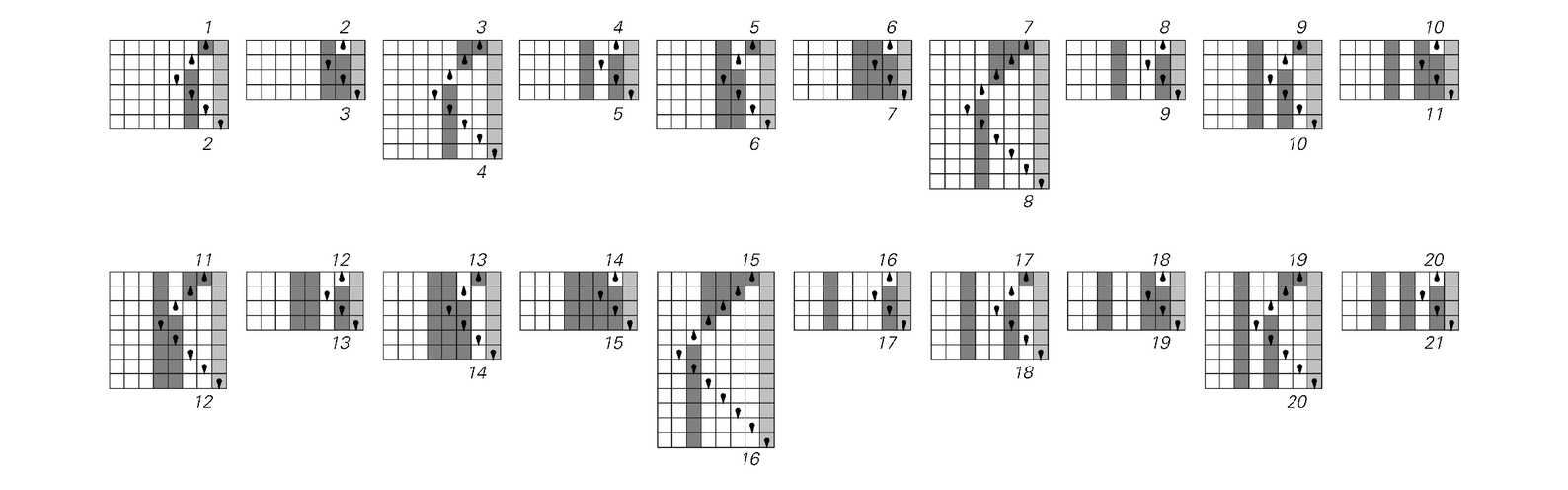
And what the pictures below show is that with this particular machine the number of steps needed to finish the computation varies greatly between different inputs. But if one looks just at the absolute maximum number of steps for any given length of input one finds an exactly linear increase with this length.

So are there other ways to do the same computation in a different number of steps? One can readily enumerate all 4096 possible Turing machines with 2 states and 2 colors. And it turns out that of these exactly 17 perform the computation of adding 1 to a number.

Each of them works in a slightly different way, but all of them follow one of the three schemes shown at the bottom of the next page—and all of them end up exhibiting the same overall linear increase in number of steps with length of input.

So what about other computations?

It turns out that there are 351 different functions that can be computed by one or more of the 4096 Turing machines with 2 states

Examples of the behavior of a simple Turing machine that does the computation of adding 1 to a number. The number is given as a base 2 digit sequence; the Turing machine runs until its head hits the gray stripe on the right. The plot shows the number of steps that this takes as a function of the input number x. The result turns out to be given by 2 IntegerExponent[x + 1, 2] + 3, which has a maximum of 2n+3, where n is the length of the digit sequence of x, or Floor[Log[2, x]]. The average for a given length of input does not increase with n, and is always precisely 5.