the outcome of an infinite number of steps in the evolution of a system like a cellular automaton.

And while these particular types of equations have never seriously been proposed as idealizations of actual processes in nature or elsewhere, it turns out that a related phenomenon can presumably occur in differential equations—which represent the most common basis for mathematical models in most areas of traditional science.

Differential equations of the kind we discussed at the end of Chapter 4 work at some level a little like cellular automata. For given the state of a system, they provide rules for determining its state at subsequent times. But whereas cellular automata always evolve only in discrete steps, differential equations instead go through a continuous process of evolution in which time appears just as a parameter.

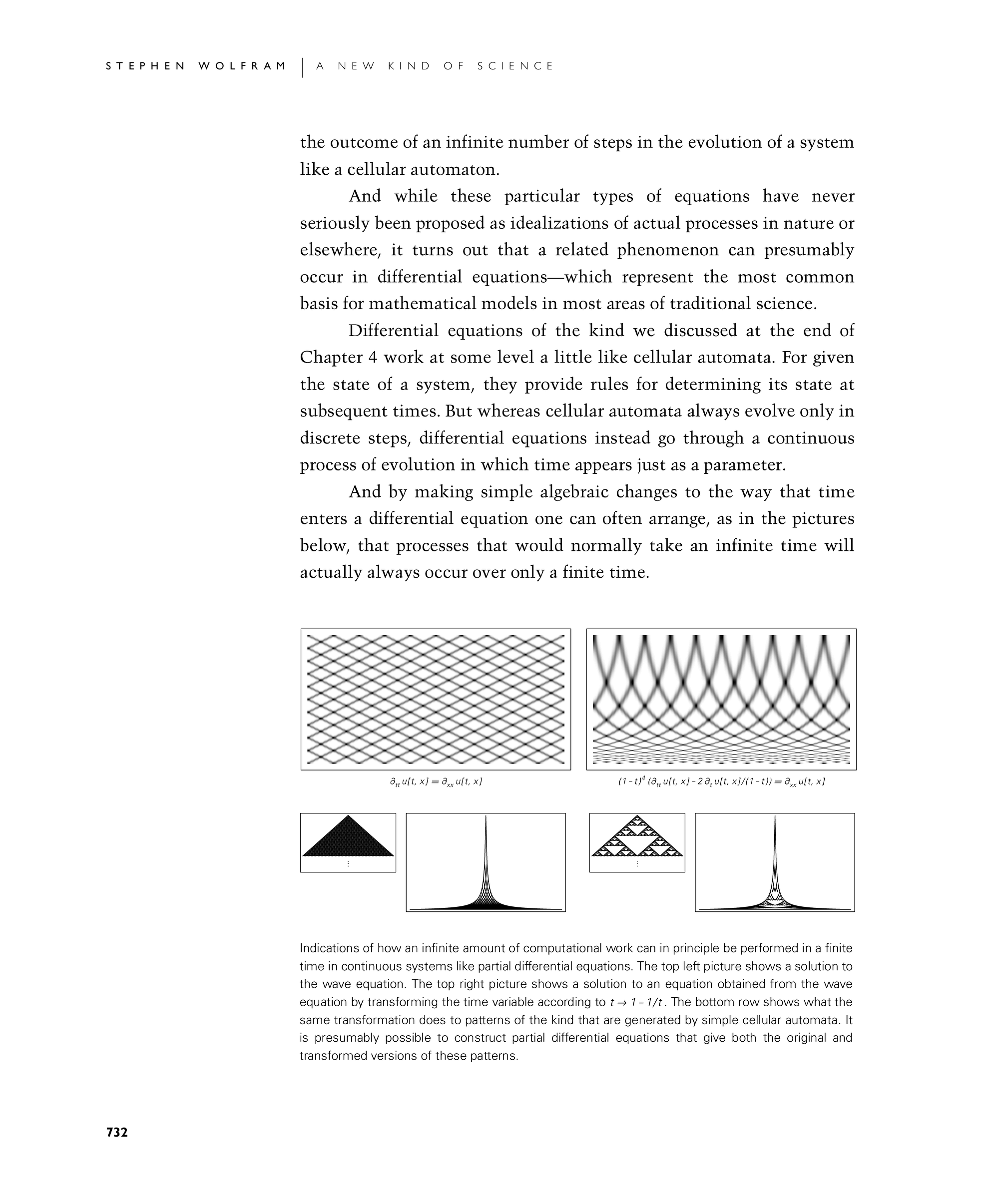
And by making simple algebraic changes to the way that time enters a differential equation one can often arrange, as in the pictures below, that processes that would normally take an infinite time will actually always occur over only a finite time.

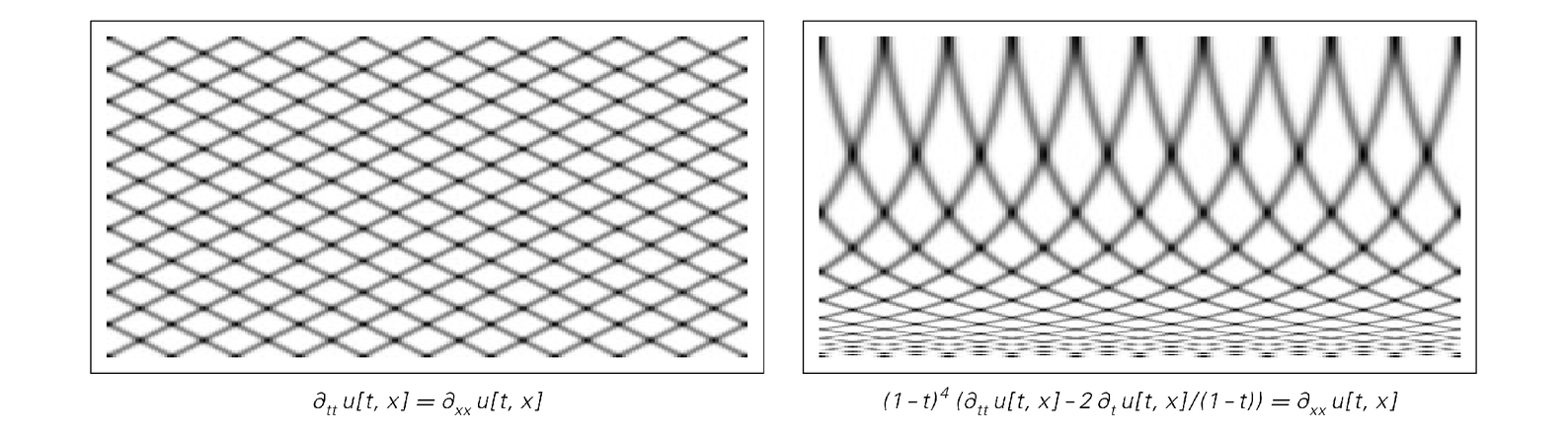
Indications of how an infinite amount of computational work can in principle be performed in a finite time in continuous systems like partial differential equations. The top left picture shows a solution to the wave equation. The top right picture shows a solution to an equation obtained from the wave equation by transforming the time variable according to t->1-1/t. The bottom row shows what the same transformation does to patterns of the kind that are generated by simple cellular automata. It is presumably possible to construct partial differential equations that give both the original and transformed versions of these patterns.