But in fact the behavior we see on the previous page is not unlike what we already saw in many elementary cellular automata a few pages back [55, 56]. Having more complicated underlying rules has not, it seems, led to much greater complexity in overall behavior.

And indeed, this is a first indication of an important general phenomenon: that at least beyond a certain point, adding complexity to the underlying rules for a system does not ultimately lead to more complex overall behavior. And so for example, in the case of cellular automata, it seems that all the essential ingredients needed to produce even the most complex behavior already exist in elementary rules.

Using more complicated rules may be convenient if one wants, say, to reproduce the details of particular natural systems, but it does not add fundamentally new features. Indeed, looking at the pictures on the previous page one sees exactly the same basic themes as in elementary cellular automata. There are some patterns that attain a definite size, then repeat forever, as shown below, others that continue to grow, but have a repetitive form, as at the top of the facing page, and still others that produce nested or fractal patterns, as at the bottom of the page.

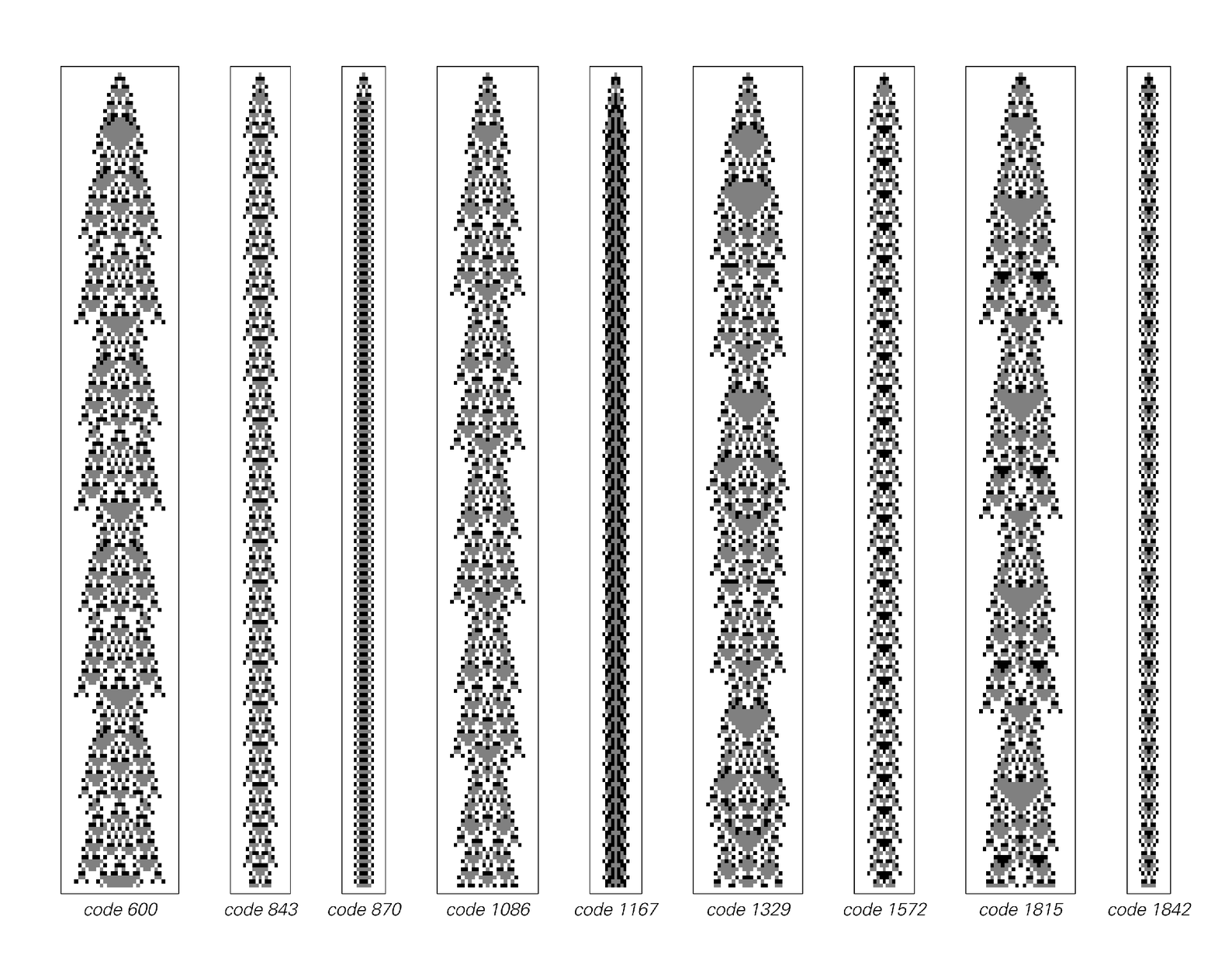
Examples of three-color totalistic rules that yield patterns which attain a certain size, then repeat forever. The maximum repetition period is found to be 78 steps, and is achieved by the rule with code number 1329. In the pictures shown here and on the following pages, the initial condition used contains a single gray cell.