But while these procedures could easily be implemented as programs, they are in a sense not based on what are traditionally thought of as ordinary mathematical functions. So is it in fact possible to get formulas for the colors of squares that involve only such functions?

In the one specific case shown at the top of the facing page it turns out to be fairly easy. For it so happens that this particular pattern—which is equivalent to the patterns at the beginning of each row on the previous page—can be obtained just by adding together pairs of numbers in the format of Pascal's triangle and then putting a black square whenever there is an entry that is an odd number.

And as the table below illustrates, the entries in Pascal's triangle are simply the binomial coefficients that appear when one expands out the powers of 1 + x. So to determine whether a particular square in the pattern is black or white, all one need do is to compute the corresponding binomial coefficient, and see whether or not it is an odd number. And this means that if black is represented by 1 and white by 0, one can then give an explicit formula for the color of the square at position x on row y: it is simply (1 - (-1)^Binomial[y, x])/2.

So what about the bottom picture on the facing page? Much as in the top picture numbers can be assigned to each square, but now these numbers are computed by successively adding together triples rather

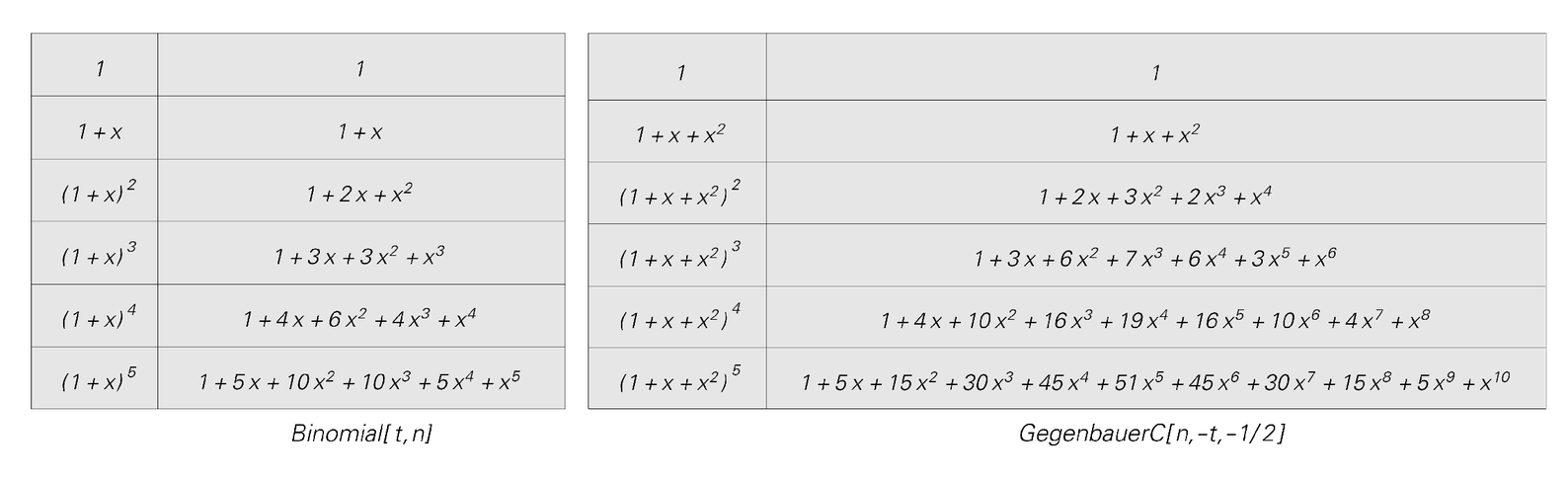
Algebraic representations of the patterns on the facing page. The coefficient of xⁿ on each row gives the value of each square. These coefficients can also be obtained from the formulas in terms of Binomial and GegenbauerC given. A particular square is colored black if its value a is odd. This can be determined either from Mod[a, 2] or equivalently from (1 - (-1)^a)/2 or Sin[π/2 a]². The succession of polynomials above can be obtained by expanding the generating functions 1/(1 - (1 + x) y) and 1/(1 - (1 + x + x²) y). Binomial[m, n] is the ordinary binomial coefficient m!/(n! (m-n)!). GegenbauerC is a so-called orthogonal polynomial—a higher mathematical function.