for the substitution system that generates a particular nested pattern, and from these construct a procedure for finding the color of a square in the pattern given its position. The pictures below show several examples, and in all cases the procedures are fairly straightforward.

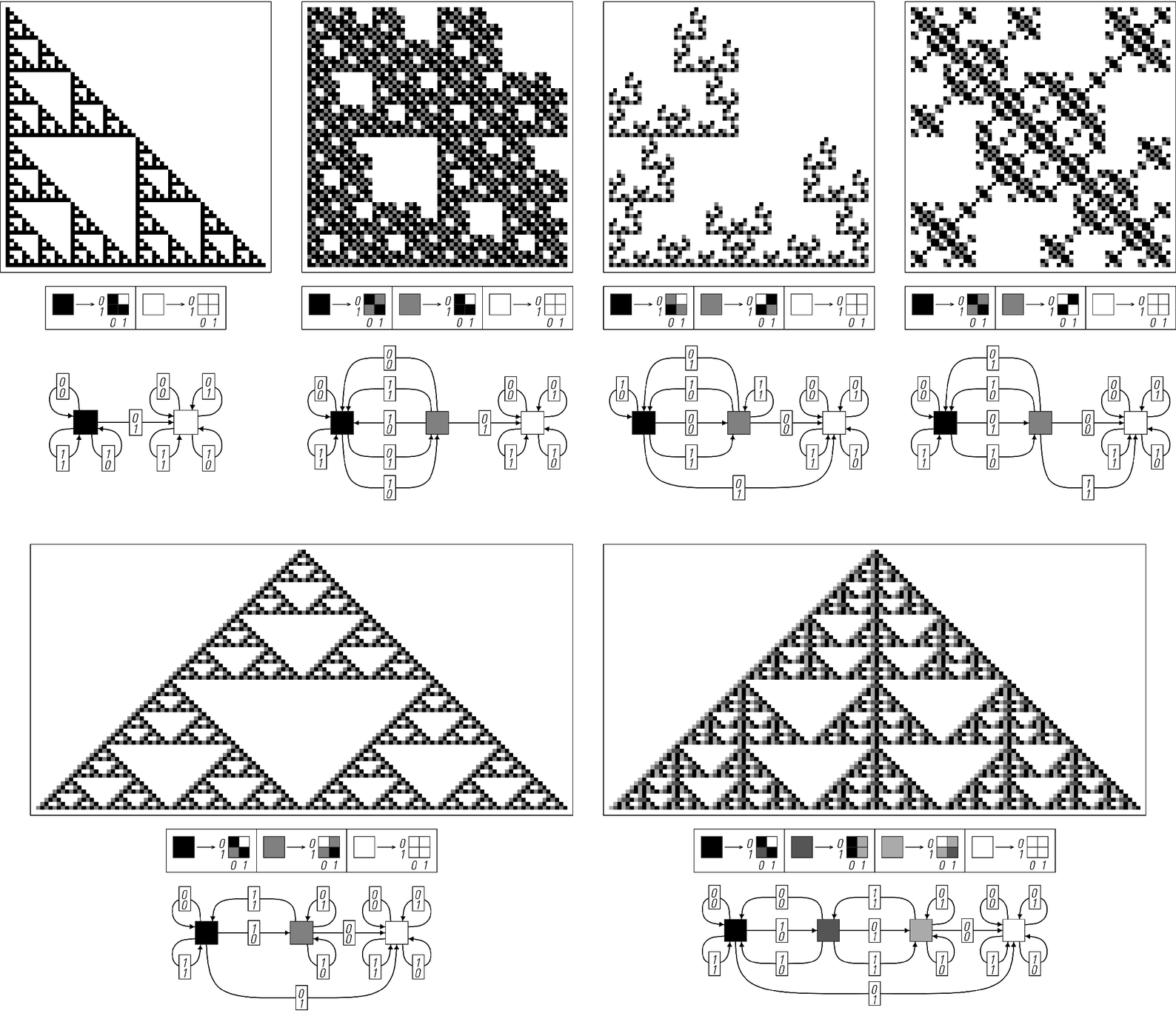
Procedures for determining the color of a square at a given position in various nested patterns. In each case the whole pattern can be generated by repeatedly applying the substitution system rule shown. The color of any particular square can also be found by feeding the digit sequences of its y and x coordinates to the finite automaton shown. The first example shown corresponds to cellular automaton rule 60; the last two examples correspond respectively to rules 90 and 150. In the top row of examples, the initial condition for the substitution system is a single black square, and the start state for the finite automaton is also its black state. In the second row of examples, the initial condition consists of a light gray square next to a black square. In these cases, the colors of squares to the left of the center can be found by starting from the light gray state in the finite automaton; the colors of squares to the right can be found by starting from the black state.