maximum likelihood, and somehow explicitly taking into account the complexity of the model itself.

For specific types of models it is possible to come up with various criteria based for example on the number of separate numerical parameters that the models contain. But in general the problem of working out what model is most appropriate for any given set of data is an extremely difficult one. Indeed, as discussed at the beginning of Chapter 8, it is in some sense the core issue in any kind of empirical approach to science.

But traditional statistical analysis is usually far from having to confront such issues. For typically it restricts itself to very specific classes of models—and usually ones which even by the standards of this book are extremely simple. For sequences of black and white squares, for example, models that work as above by just assigning probabilities to fixed blocks of squares are by far the most common. An alternative, typically viewed as quite advanced, is to assign probabilities to sequences by looking at the paths that correspond to these sequences in networks of the kind shown below.

Networks (a) and (b) represent cases already discussed above. Network (a) specifies that the colors of successive squares should be chosen independently, while network (b) specifies that this should be done for successive pairs of squares. Network (c), however, specifies that different probabilities should be used depending on whether the path has reached the left or the right node in the network. But at least

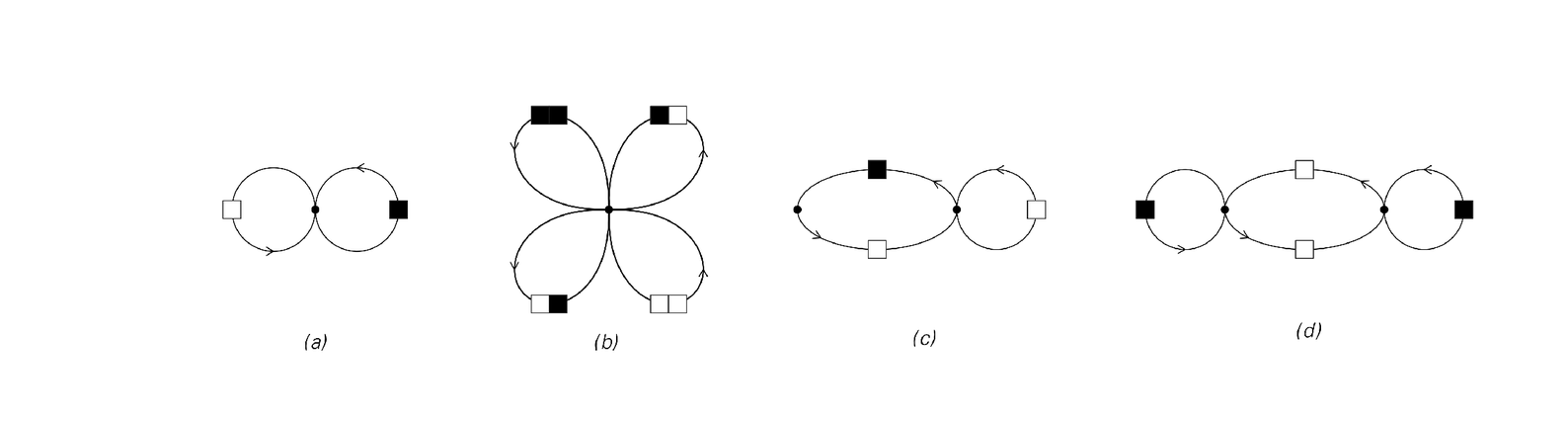
Networks defining probabilistic models. Each connection in each network has a certain probability associated with it, and the model takes sequences of black and white squares to be generated by tracing paths through the networks according to these probabilities. Cases (a) and (b) are so-called Markov models that in effect involve no memory and are equivalent to models discussed above. Cases (c) and (d) correspond to so-called hidden Markov models, with some short-term memory.