followed by a specification of the length of the sequence that the object describes. In the first kind of object, the actual sequence is then given, while in the second kind of object what is given is a specification of how far back in the data the required sequence can be found.

With data that is purely repetitive this method achieves quite dramatic compression. For having once specified the basic sequence to be repeated, all that then needs to be given is a pointer to this sequence, together with a representation of the total length of the data.

Purely nested data can also be compressed nearly as much. For as the pictures below illustrate, each whole level of nesting can be viewed just as adding a fixed number of repeated sequences.

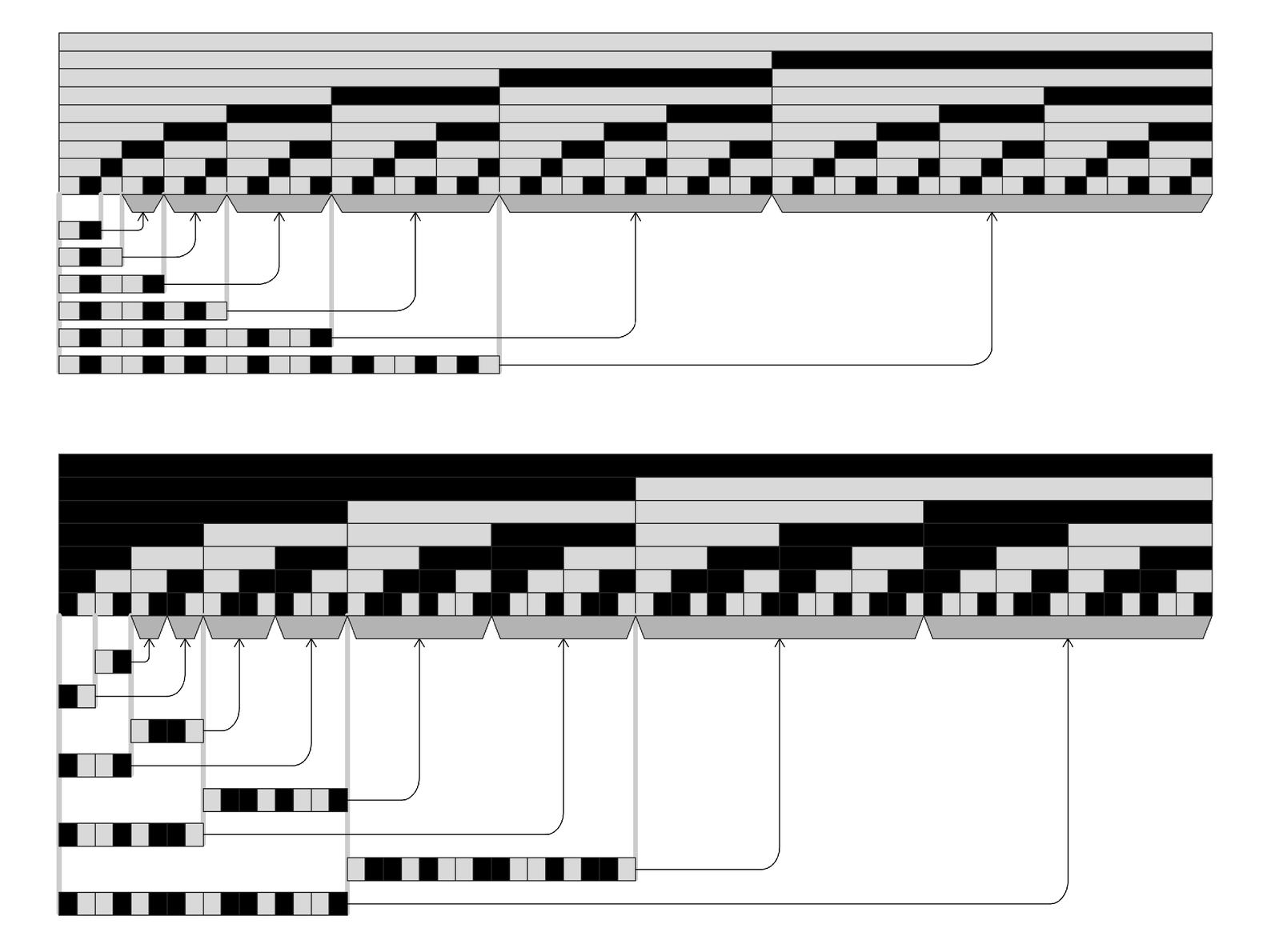
Examples of the pattern of repeats found in purely nested data. As indicated in these pictures, any such data must correspond to the output of a neighbor-independent substitution system (see page 83). In pointer-based encoding, the number of pointers required to represent the data increases essentially like the number of steps in the evolution of the substitution system. Taking into account the length of the representation for each pointer, the compressed form of a nested sequence of length n will typically grow in length like Log[n]². (This can be compared with Log[n] growth for a purely repetitive sequence.) Note that actual algorithms for pointer-based encoding will typically find a slightly less regular pattern of repeats than is shown in the pictures here.