Elementary Particles

There are some aspects of the universe—notably the structure of space and time—that present-day physics tends to assume are continuous. But over the past century it has at least become universally accepted that all matter is made up of identifiable discrete particles.

Experiments have found a fairly small number of fundamentally different kinds of particles, with electrons, photons, muons and the six basic types of quarks being a few examples. And it is one of the striking observed regularities of the universe that all particles of a given kind—say electrons—seem to be absolutely identical in their properties.

But what actually are particles? As far as present-day experiments can tell, electrons, for example, have zero size and no substructure. But particularly if space is discrete, it seems almost inevitable that electrons and other particles must be made up of more fundamental elements.

So how might this work? An immediate possibility that I suspect is actually not too far from the mark is that such particles are analogs of the localized structures that we saw earlier in this book in systems like the class 4 cellular automata shown below. And if this is so, then it means that at the lowest level, the rules for the universe need make no reference to particular particles. Instead, all the particles we see would just emerge as structures formed from more basic elements.

In networks it can be somewhat difficult to visualize localized structures. But the picture below nevertheless shows a simple example of how a localized structure can move across a regular planar network.

Both the examples on this page show structures that exist on very regular backgrounds. But to get any kind of realistic model for actual

Typical examples of particle-like localized structures in class 4 cellular automata.

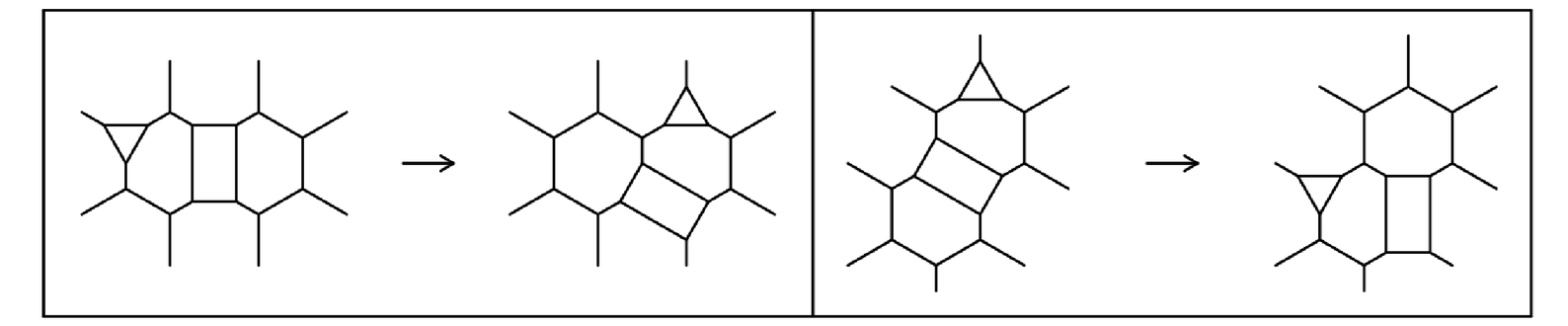
A particle-like localized structure in a network.