choice of whether actually to perform a given replacement at a particular step, or whether to delay that replacement until a subsequent step. But what must be true is that there can never be any ambiguity about what replacement will eventually be made in any given part of the system.

In rules like the ones at the top of page 500 where each replacement involves just a single element this is inevitably how things must work. But what about rules that have replacements involving blocks of more than one element? Can such rules still have the necessary properties?

The pictures below show two examples of rules that do. In the first picture for each rule, replacements are made at randomly chosen steps, while in the second picture, they are in a sense always made at the earliest possible step. But the point is that in no case is there any ambiguity about what replacement will eventually be made at any particular place in the system. And as a result, the causal network that represents the relationships between different updating events is always exactly the same.

So what underlying property must the rules for a substitution system have in order to make the system as a whole operate in this way? The basic answer is that somehow different replacements must never be able to interfere with each other. And one way to guarantee this is if the blocks involved in replacements can never overlap.

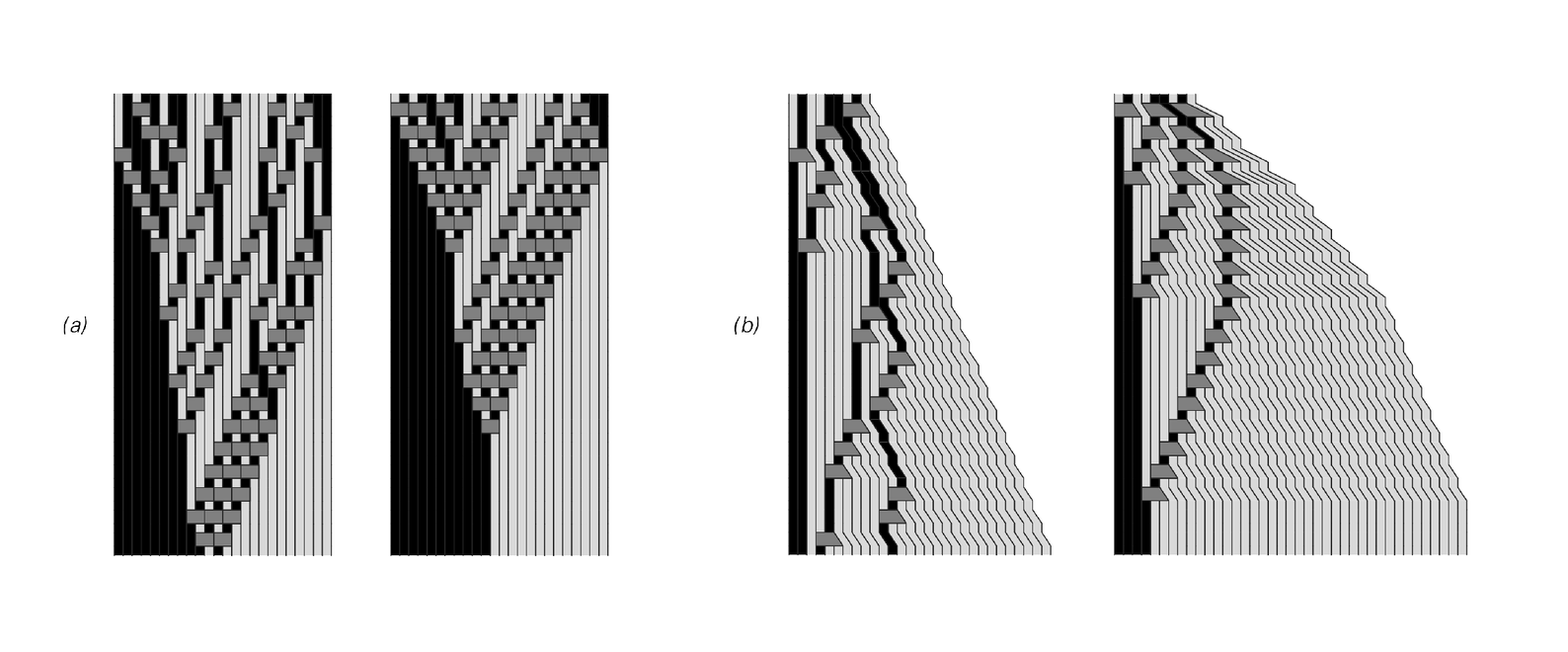
Examples of substitution systems in which the same causal networks are obtained regardless of the way in which replacements are performed. In the first picture for each rule, the replacements are performed essentially at random. In the second picture they are performed on the earliest possible step. Note that rule (a) effectively sorts the elements in its initial conditions, always placing black before white.