One may wonder, however, to what extent the behavior one sees depends on the exact scheme that one uses to pick which replacements to apply at each step. The answer is that for the vast majority of rules—including rules (c) through (g) in the picture on the facing page—using different schemes yields quite different behavior—and a quite different causal network.

But remarkably enough there do exist rules for which exactly the same causal network is obtained regardless of what scheme is used. And as it turns out, rules (a) and (b) from the picture on the facing page provide simple examples of this phenomenon, as illustrated in the pictures below.

For each rule, the three different pictures in the first image below correspond to three different ways that replacements can be made. And while the positions of particular updating events are different in every picture, the point is that the network of causal connections between these events is always exactly the same.

This is certainly not true for every substitution system. Indeed, the pictures in the second image show how it can fail, for example, for rule (e) from the facing page. What one sees in these pictures is that after event 4, different choices of replacements are made in the two cases, and the causal relationships implied by these replacements are different.

So what could ensure that no such situation would ever arise in a particular substitution system? Essentially what needs to be true is that the sequence of elements alone must always uniquely determine what replacements can be made in every part of the system. One still has a

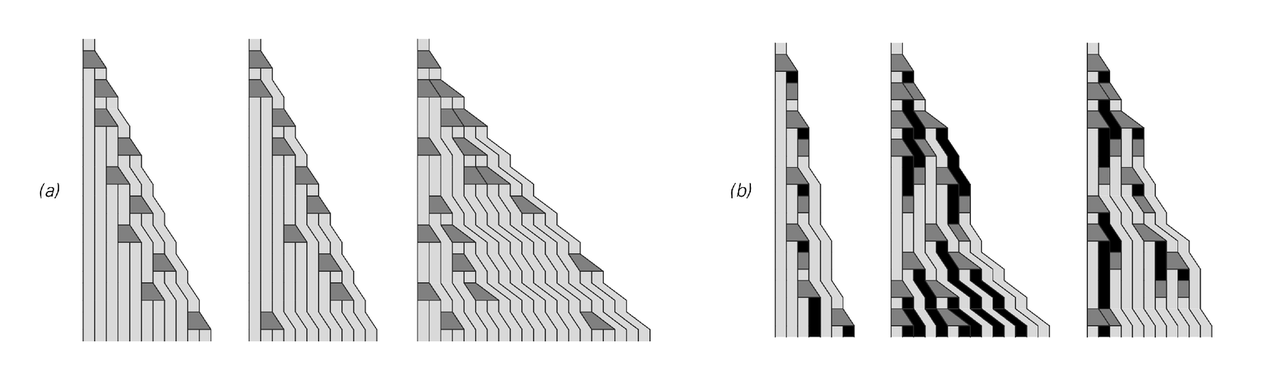
The behavior of rules (a) and (b) from the facing page when replacements are performed at random. Even though the detailed patterns obtained are different, the causal networks in these particular rules that represent relationships between replacement events are always exactly the same.

Examples of two different ways of performing replacements in rule (e) from the facing page, yielding two different causal networks.