of the causal networks for rules (e) and (f) requires following the underlying mobile automaton evolution for 2447 and 731 steps respectively.

One feature of causal networks is that they tell one not only what the consequences of a particular event will be, but also in a sense what its causes were. Thus, for example, if one starts, say, with event 17 in the first causal network below, then to find out that its causes were events 11 and 16 one simply has to trace backwards along the connections which lead to it.

With the specific type of underlying mobile automaton used here, every node has exactly three incoming and three outgoing connections. And at least when there is overall apparent randomness, the networks that one gets by going forwards and backwards from a particular node will look very similar. In most cases there will still be small differences; but the causal network on the right below is specifically constructed to be exactly reversible—much like the cellular automata we discussed near the beginning of this chapter.

Looking at the causal networks we have seen so far, one may wonder to what extent their form depends on the particular properties of the underlying mobile automata that were used to produce them.

For example, one might think that the fact that all the networks we have seen so far grow at most linearly with time must be an inevitable consequence of the one-dimensional character of the mobile

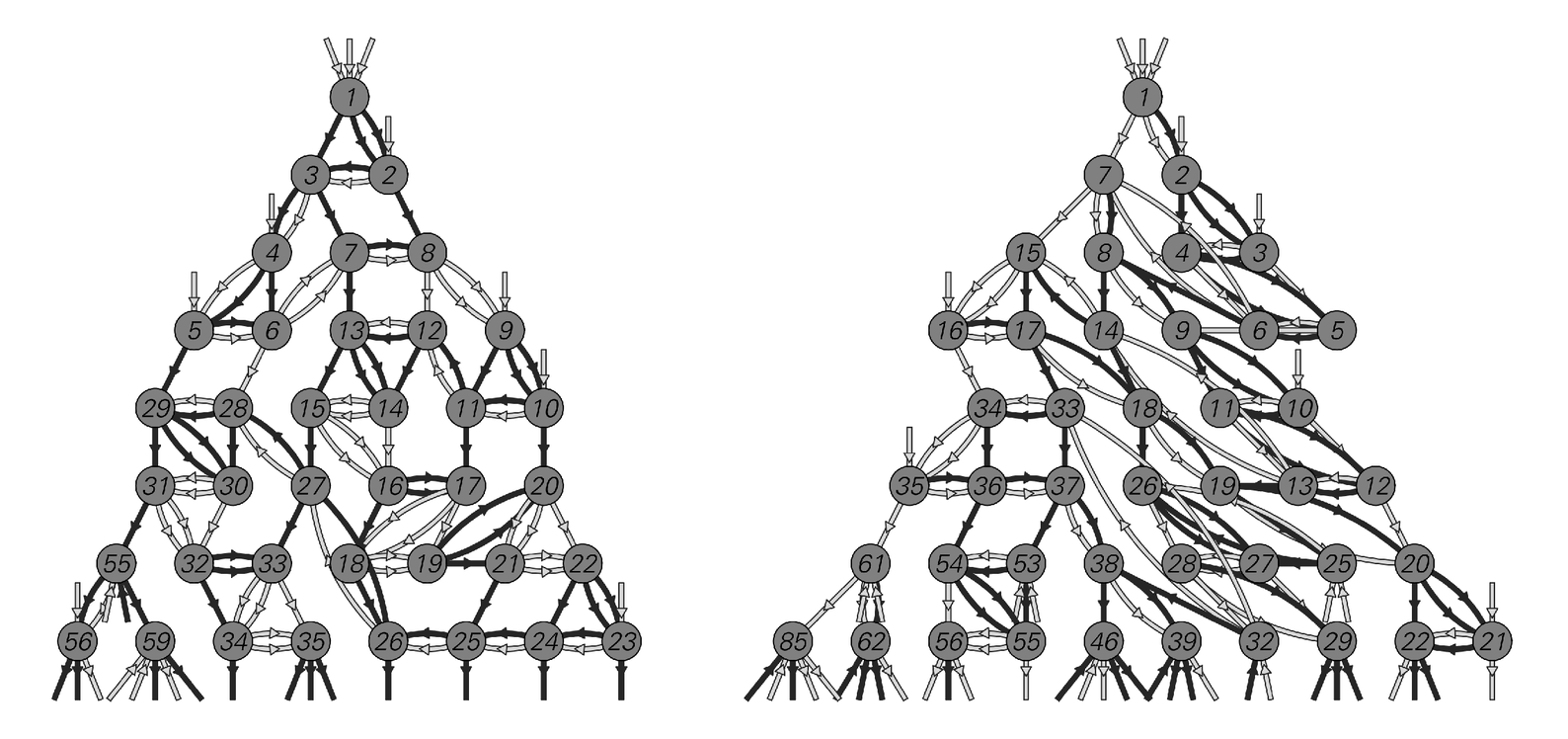
Causal networks corresponding to rules (e) and (f) from page 493, with each node explicitly labelled to specify from which step of mobile automaton evolution it is derived. Even to fill in the first few rows of such causal networks, many steps of underlying mobile automaton evolution must be traced.