So even though the total of the energy of all particles remains the same, the distribution of this energy becomes progressively more random, just as the usual Second Law implies.

An important practical consequence of this is that it becomes increasingly difficult to extract energy from the system in the form of systematic mechanical work. At an idealized level one might imagine trying to do this by inserting into the system some kind of paddle which would experience force as a result of impacts from particles.

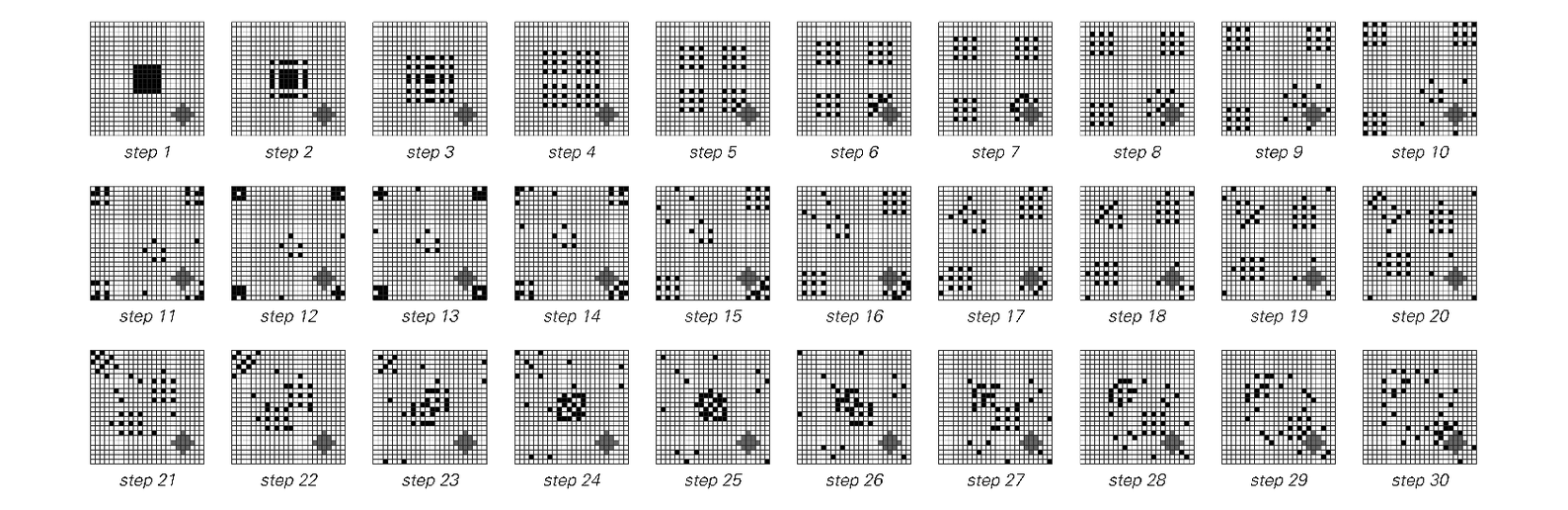
The behavior of a simple two-dimensional cellular automaton that emulates an ideal gas of particles. In the top group of pictures, the particles bounce around in an empty square box. In the bottom group of pictures, the box contains a small fixed obstacle. In the top group of pictures, the arrangement of particles shows simple repetitive behavior. In the bottom group, however, it becomes progressively more random with time. The underlying rules for the cellular automaton used here are reversible, and conserve the total number of particles. The specific rules are based on 2×2 blocks—a two-dimensional generalization of the block cellular automata to be discussed in the next section. For each 2×2 block the configuration of particles is taken to remain the same at a particular step unless there are exactly two particles arranged diagonally within the block, in which case the particles move to the opposite diagonal.