much more reflect explicit rules of evolution than the constraint associated with the invariant state.

So what about actual systems in physics? Do they behave any differently? As one example, consider a large number of circular coins pushed together on a table. One can think of such a system as having an invariant state that satisfies the constraint that the coins should be packed as densely as possible. For identical coins this constraint is satisfied by the simple repetitive pattern shown on the right. And it turns out that in this particular case this pattern is quickly produced if one actually pushes coins together on a table.

But with balls in three dimensions the situation is quite different. In this case the constraint of densest packing is known to be satisfied when the balls are laid out in the simple repetitive way shown on the right. But if one just tries pushing balls together they almost always get stuck, and never take on anything like the arrangement shown. And if one jiggles the balls around one still essentially never gets this arrangement. Indeed, the only way to do it seems to be to lay the balls down carefully one after another.

In two dimensions similar issues arise as soon as one has coins of more than one size. Indeed, even with just two sizes, working out how to satisfy the constraint of densest packing is already so difficult that in most cases it is still not known what configuration does it.

Typical behavior of two-dimensional cellular automata that leave only the pattern on the right invariant. The results shown come from 500 steps of evolution starting from random initial conditions. In no case does the global behavior seen come even close to satisfying the simple constraints that determine the invariant state.

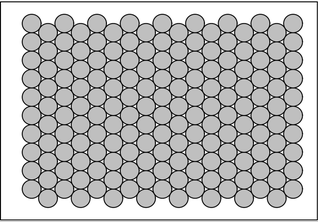
The densest packing of identical circles in the plane. Each circle is surrounded by six others.

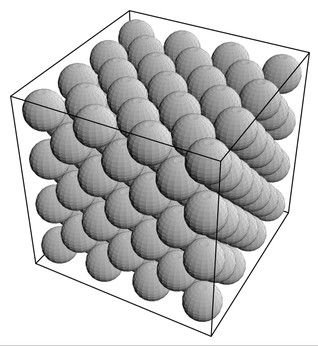
The densest packing of identical spheres in three-dimensional space. Each sphere is surrounded by 12 others.