
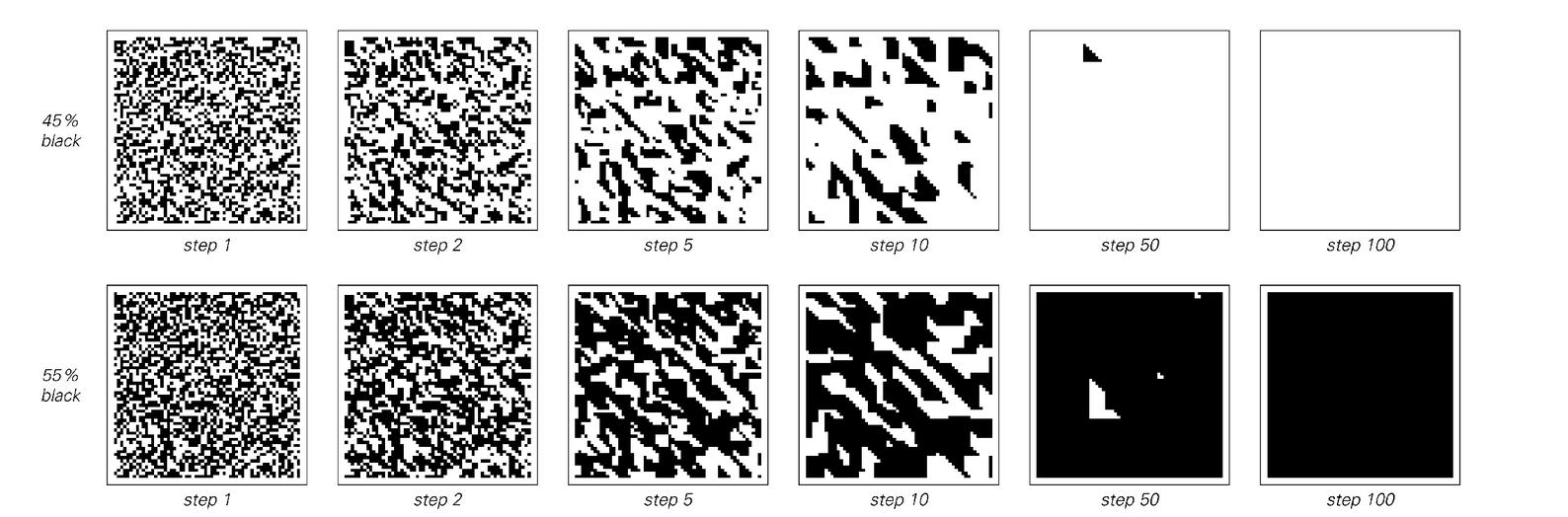

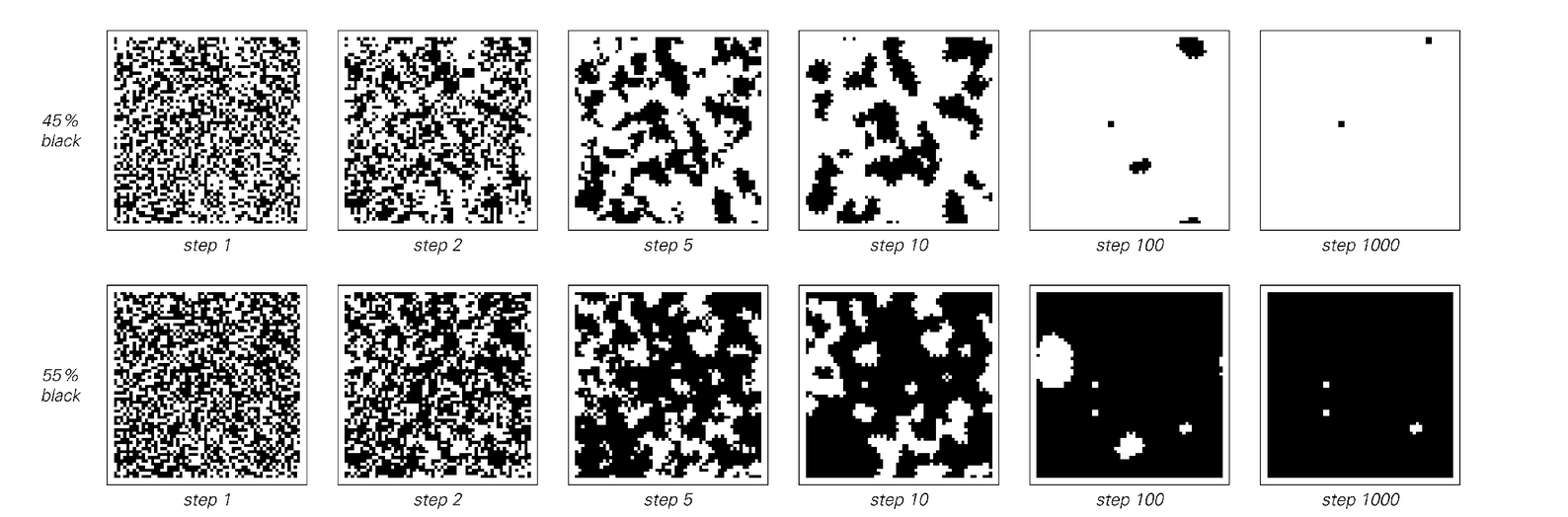
Two examples of two-dimensional cellular automata that show discrete transitions in behavior when the density of initial black cells is continuously varied. In the top rule, the new color of a particular cell is found simply by looking at that cell and its immediate neighbors above and to the right. If two or more of these three cells are black, then the new color is black; otherwise it is white. The pictures in the middle above show that with this rule blocks of opposite color are progressively destroyed, so that whichever color was initially more common eventually dominates completely. The bottom rule above is exactly the same as was shown on page 336. Whichever color was initially more common again eventually dominates, though with this rule it takes somewhat longer for this to occur.



