they become increasingly common. The pictures on the next page show two examples—the second corresponding to a rule that we saw in a different context at the end of the previous section.

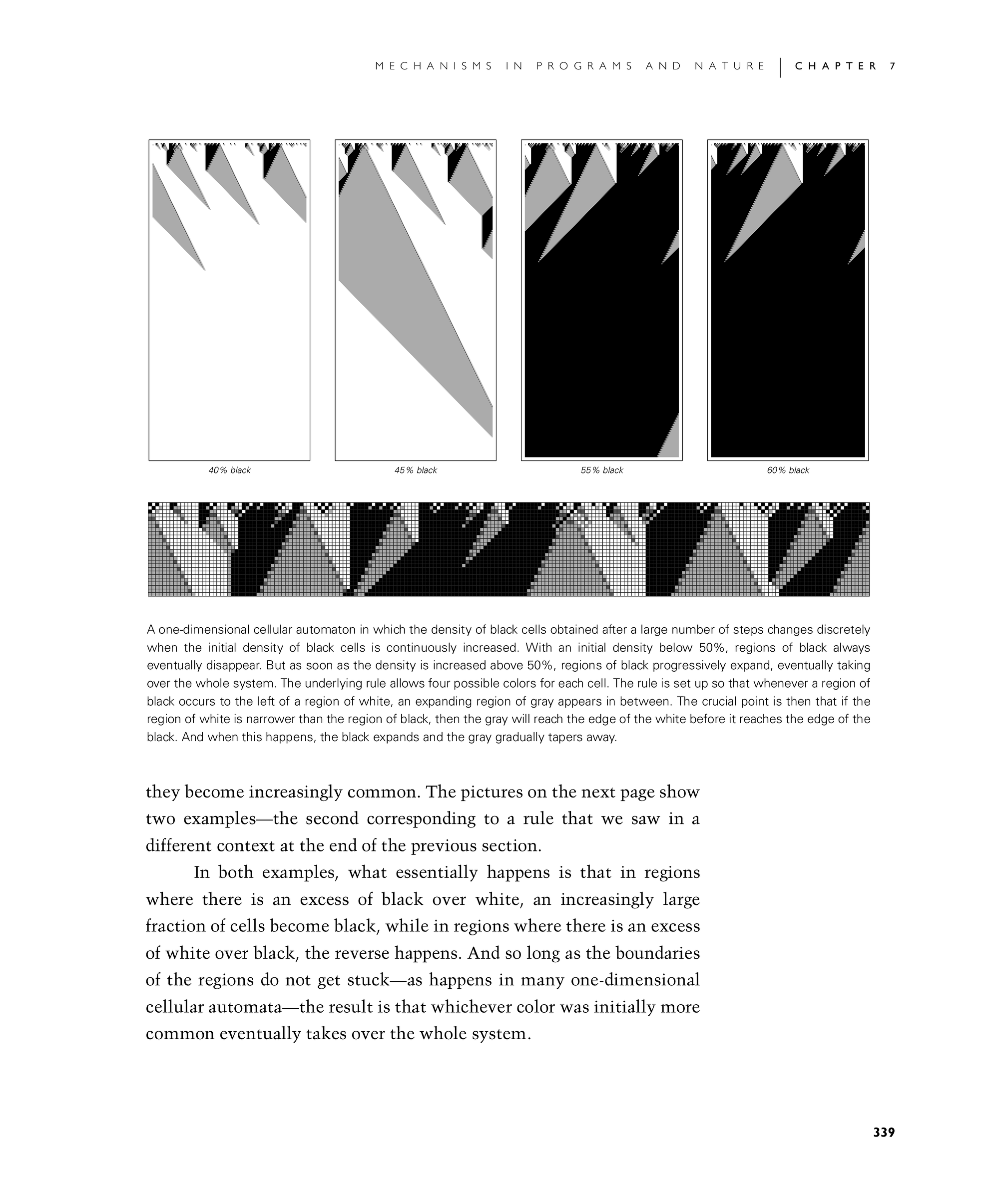
In both examples, what essentially happens is that in regions where there is an excess of black over white, an increasingly large fraction of cells become black, while in regions where there is an excess of white over black, the reverse happens. And so long as the boundaries of the regions do not get stuck—as happens in many one-dimensional cellular automata—the result is that whichever color was initially more common eventually takes over the whole system.

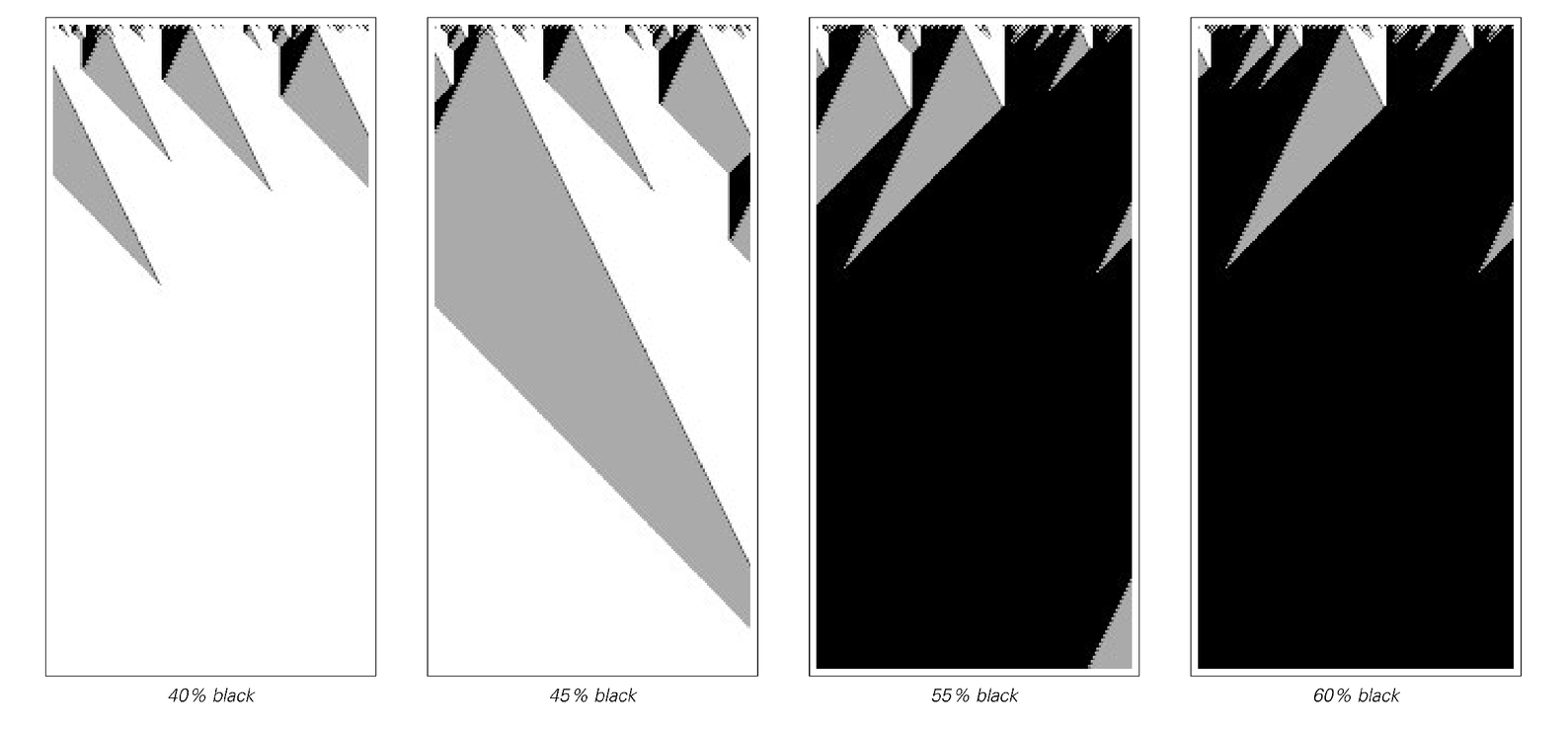
A one-dimensional cellular automaton in which the density of black cells obtained after a large number of steps changes discretely when the initial density of black cells is continuously increased. With an initial density below 50%, regions of black always eventually disappear. But as soon as the density is increased above 50%, regions of black progressively expand, eventually taking over the whole system. The underlying rule allows four possible colors for each cell. The rule is set up so that whenever a region of black occurs to the left of a region of white, an expanding region of gray appears in between. The crucial point is then that if the region of white is narrower than the region of black, then the gray will reach the edge of the white before it reaches the edge of the black. And when this happens, the black expands and the gray gradually tapers away.