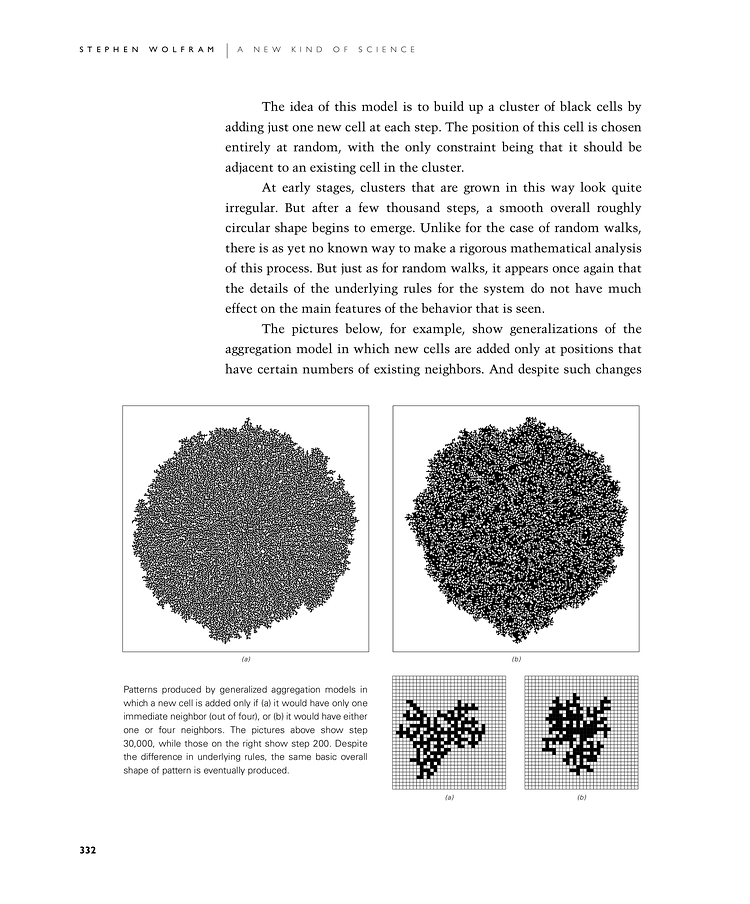
The idea of this model is to build up a cluster of black cells by adding just one new cell at each step. The position of this cell is chosen entirely at random, with the only constraint being that it should be adjacent to an existing cell in the cluster.

At early stages, clusters that are grown in this way look quite irregular. But after a few thousand steps, a smooth overall roughly circular shape begins to emerge. Unlike for the case of random walks, there is as yet no known way to make a rigorous mathematical analysis of this process. But just as for random walks, it appears once again that the details of the underlying rules for the system do not have much effect on the main features of the behavior that is seen.

The pictures below, for example, show generalizations of the aggregation model in which new cells are added only at positions that have certain numbers of existing neighbors. And despite such changes

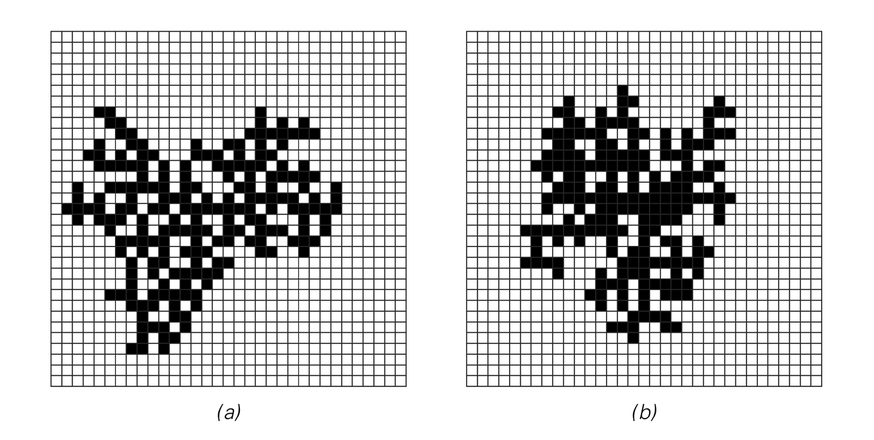
Patterns produced by generalized aggregation models in which a new cell is added only if (a) it would have only one immediate neighbor (out of four), or (b) it would have either one or four neighbors. The top pictures show step 30,000, while those on the bottom right show step 200. Despite the difference in underlying rules, the same basic overall shape of pattern is eventually produced.