becomes possible. And indeed, the pictures on the next two pages [202, 203] show examples of what can happen if the rules are allowed to depend on the number of distinct nodes reached by following not just one but up to two successive connections from each node.

With such rules, the sequence of networks obtained no longer needs to form any kind of simple progression, and indeed one finds that even the total number of nodes at each step can vary in a way that seems in many respects completely random.

When we discuss issues of fundamental physics in Chapter 9 we will encounter a variety of other types of network systems—and I suspect that some of these systems will in the end turn out to be closely related to the basic structure of space and spacetime in our universe.

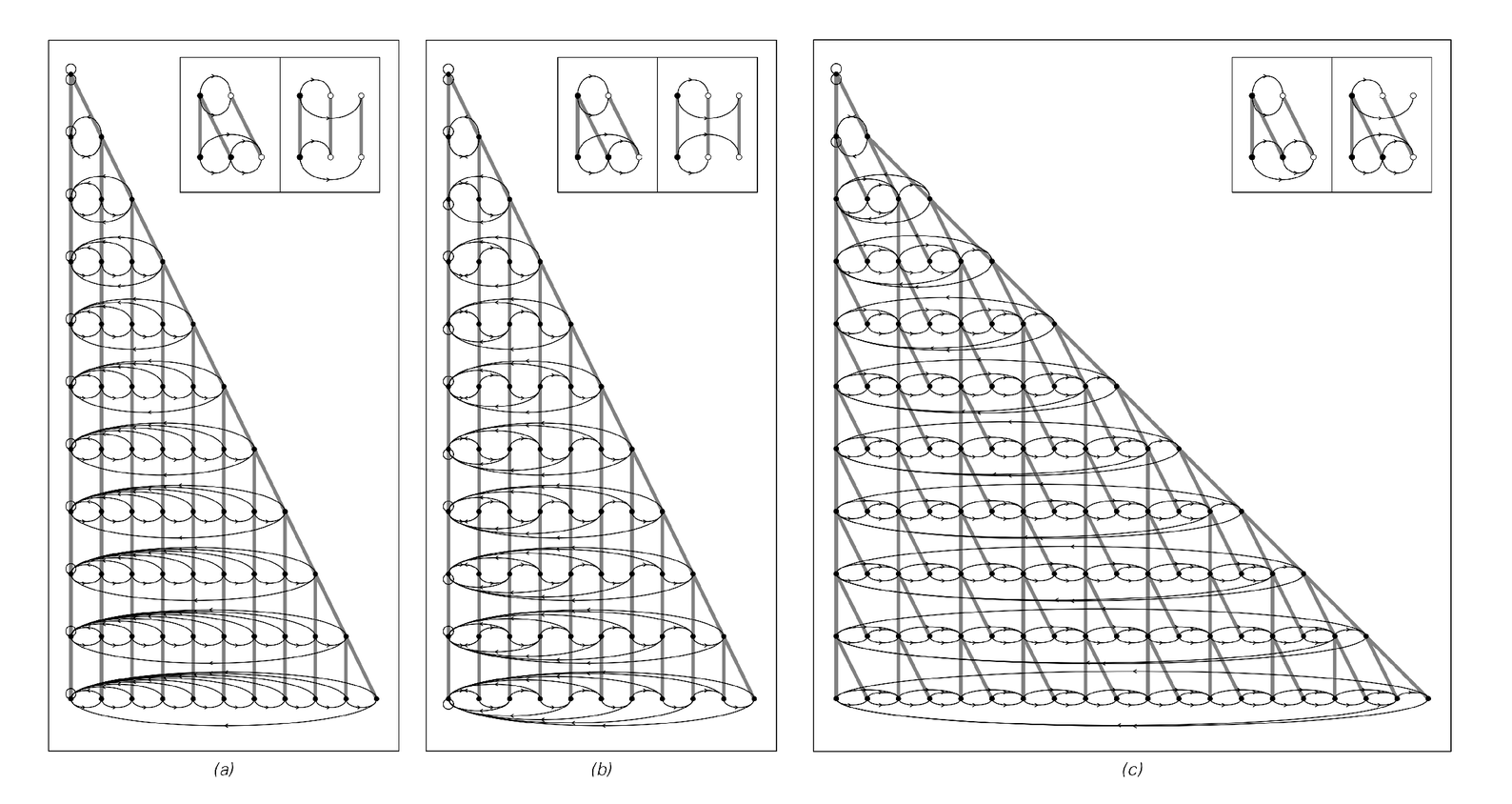
Examples of network systems with rules that cause different operations to be performed at different nodes. Each rule contains two cases, as shown above. The first case specifies what to do if both connections from a particular node lead to the same node; the second case specifies what to do when they lead to different nodes. In the rules shown, the connections from a particular node (indicated by a solid circle) and from new nodes created from this node always go to the nodes indicated by open circles that are reached by following just a single above or below connection from the original node. Even if this restriction is removed, however, more complicated behavior does not appear to be seen.