Name: A New Kind of Science
Author: Stephen Wolfram
ISBN: 1-57955-008-8

Example (c) then shows that with appropriate connections, it is also possible to get a three-dimensional array, and indeed using the same principles an array with any number of dimensions can easily be obtained.

The pictures below show examples of networks that form infinite trees rather than arrays. Notice that the first and last networks shown actually have an identical pattern of connections, but they look different here because the nodes are arranged in a different way on the page.

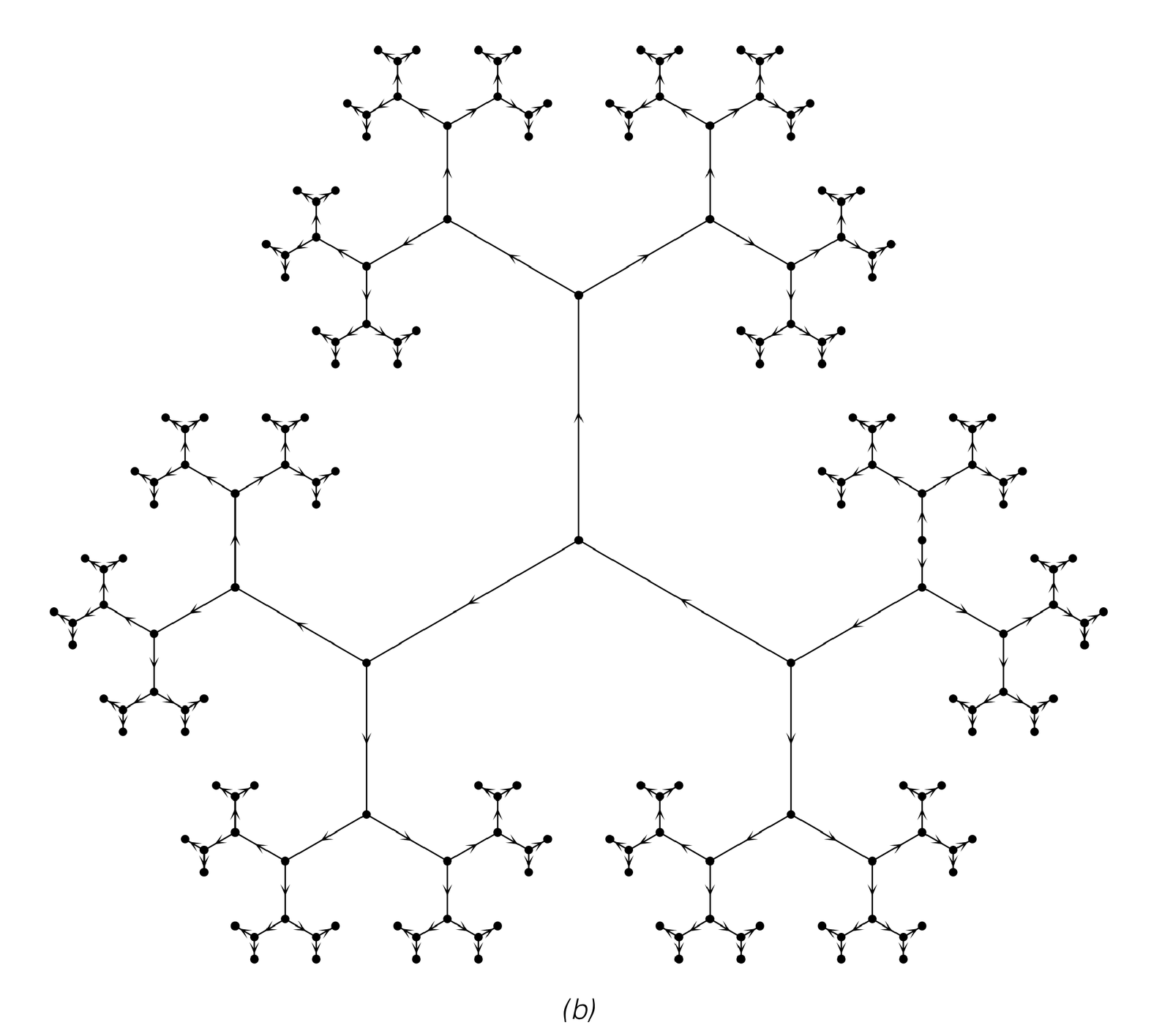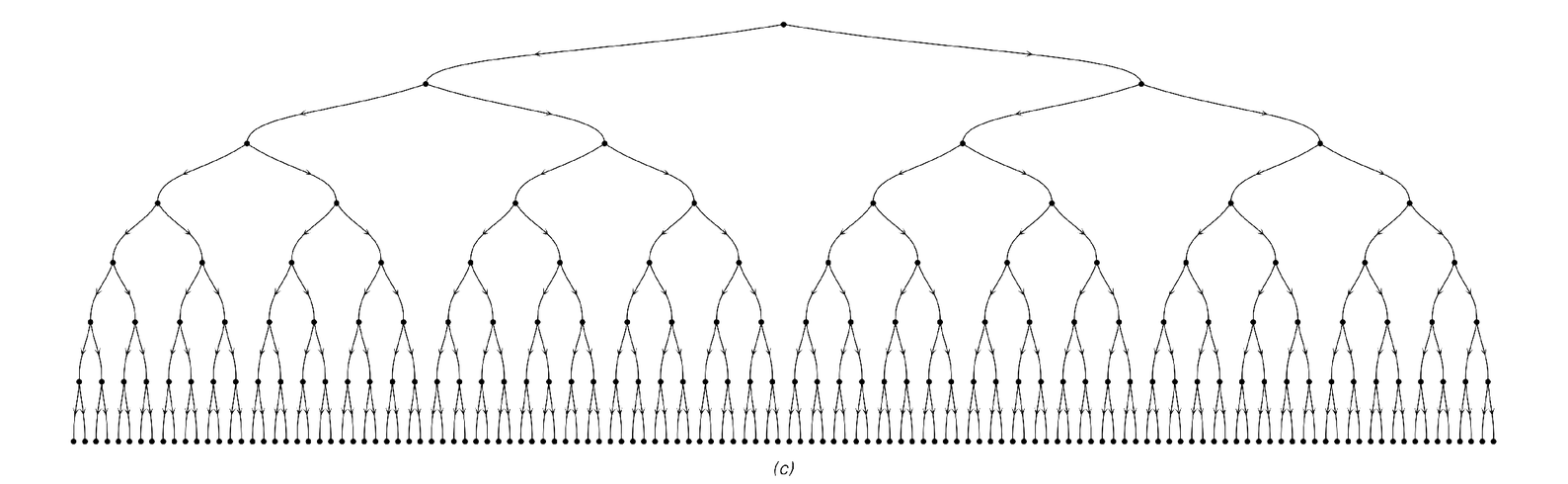
Networks corresponding to infinite trees — Examples of networks that correspond to infinite trees. Note that networks (a) and (c) are identical, though they look different because the nodes are laid out differently on the page. All the networks shown are truncated at the leaves of each tree.

Networks corresponding to infinite trees 2 — Examples of networks that correspond to infinite trees. Note that networks (a) and (c) are identical, though they look different because the nodes are laid out differently on the page. All the networks shown are truncated at the leaves of each tree.