So how can this be generalized to higher dimensions? On a two-dimensional grid one can certainly imagine snaking backwards and forwards or spiralling outwards to scan all the elements. But as soon as one defines any particular order for elements—however they may be laid out—this in effect reduces one to dealing with a one-dimensional system.
And indeed there seems to be no immediate way to generalize sequential substitution systems to two or more dimensions. In Chapter 9, however, we will see that with more sophisticated ideas it is in fact possible in any number of dimensions to set up substitution systems in which elements are scanned in order—but whatever order is used, the results are in some sense always the same.

A two-dimensional neighbor-dependent substitution system. The grid of cells is assumed to wrap around in both its dimensions.
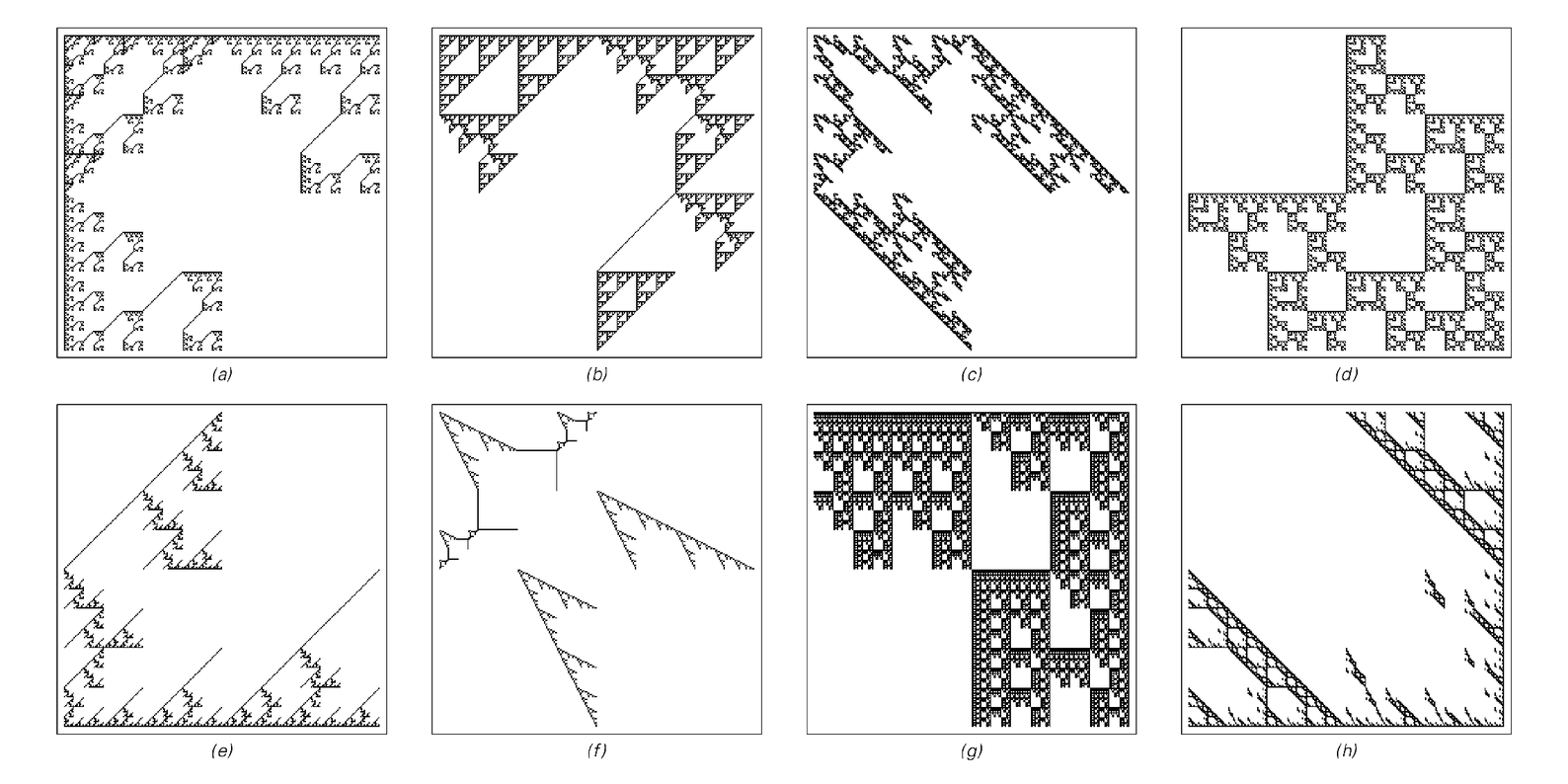

Patterns generated by 8 steps of evolution in various two-dimensional neighbor-dependent substitution systems.



