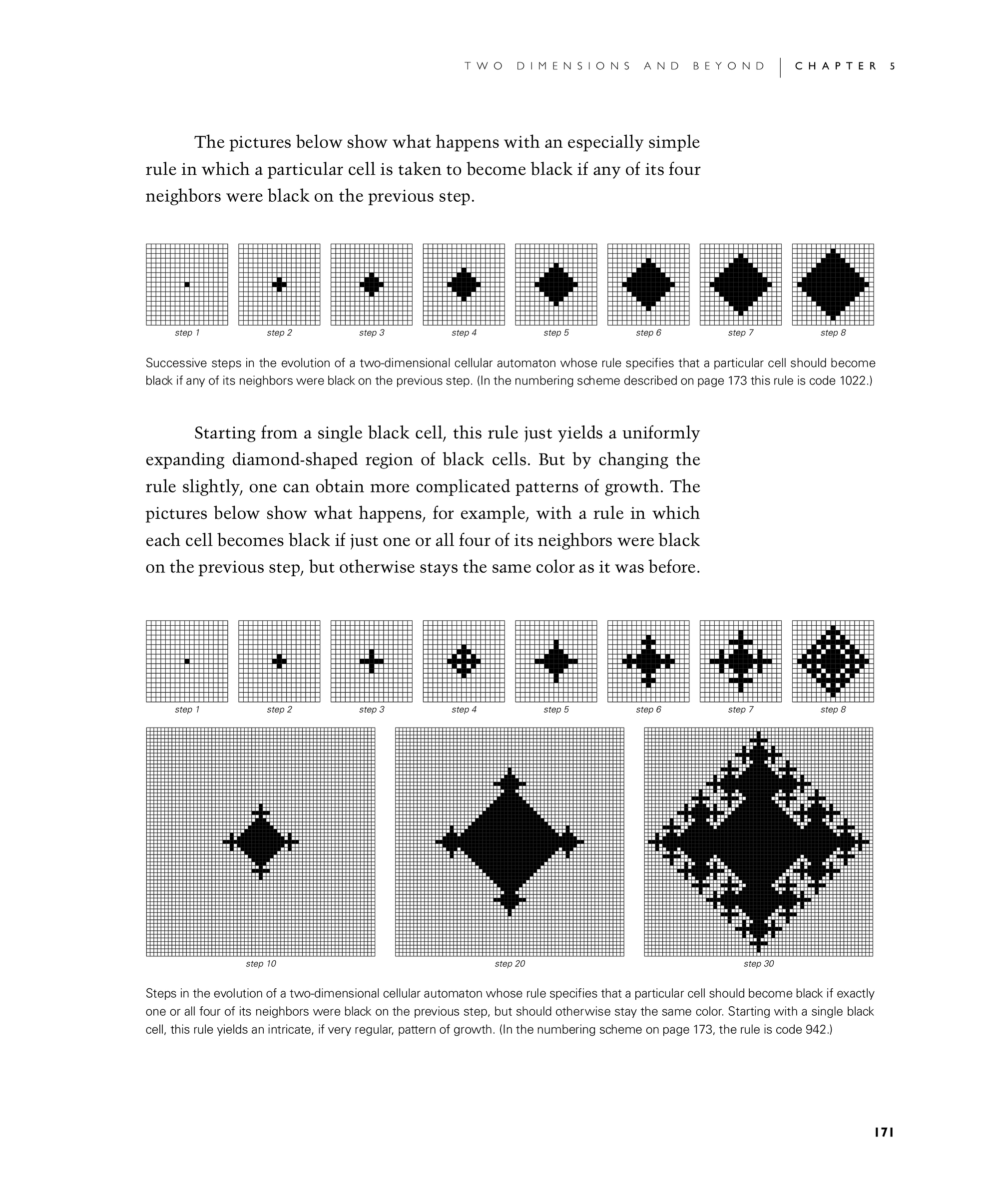
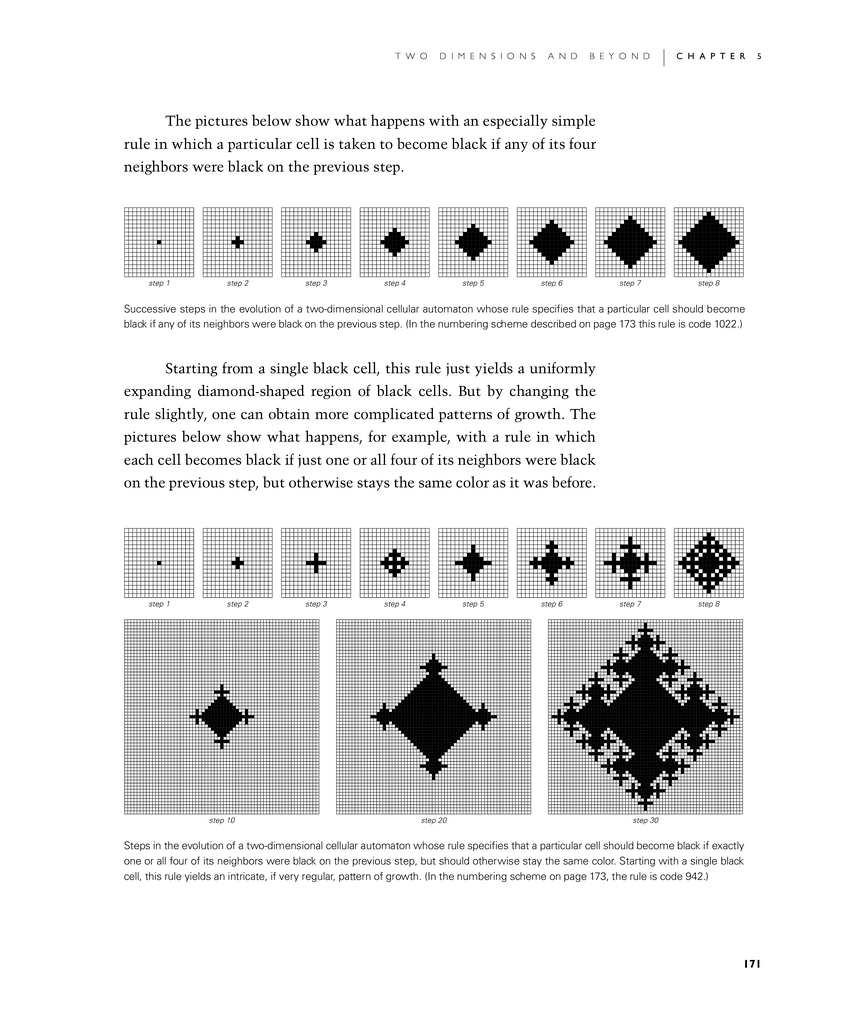
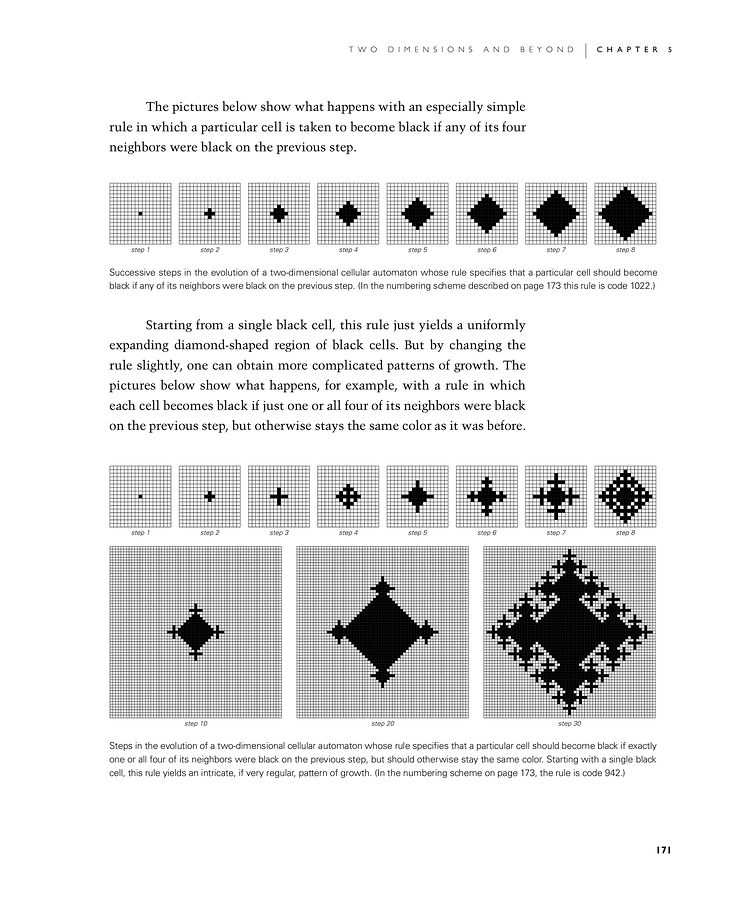
The first set of pictures below show what happens with an especially simple rule in which a particular cell is taken to become black if any of its four neighbors were black on the previous step.

Starting from a single black cell, this rule just yields a uniformly expanding diamond-shaped region of black cells. But by changing the rule slightly, one can obtain more complicated patterns of growth. The second set of pictures below show what happens, for example, with a rule in which each cell becomes black if just one or all four of its neighbors were black on the previous step, but otherwise stays the same color as it was before.

Successive steps in the evolution of a two-dimensional cellular automaton whose rule specifies that a particular cell should become black if any of its neighbors were black on the previous step. (In the numbering scheme described on page 173 this rule is code 1022.)

Steps in the evolution of a two-dimensional cellular automaton whose rule specifies that a particular cell should become black if exactly one or all four of its neighbors were black on the previous step, but should otherwise stay the same color. Starting with a single black cell, this rule yields an intricate, if very regular, pattern of growth. (In the numbering scheme on page 173, the rule is code 942.)