| |
SOME HISTORICAL NOTES

From: Stephen Wolfram, A New Kind of Science
Notes for Chapter 2: The Crucial Experiment
Section: Why These Discoveries Were Not Made Before
Page 876
History of cellular automata. Despite their very simple construction, nothing like general cellular automata appear to have been considered before about the 1950s. Yet in the 1950s - inspired in various ways by the advent of electronic computers - several different kinds of systems equivalent to cellular automata were independently introduced. A variety of precursors can be identified. Operations on sequences of digits had been used since antiquity in doing arithmetic. Finite difference approximations to differential equations began to emerge in the early 1900s and were fairly well known by the 1930s. And Turing machines invented in 1936 were based on thinking about arbitrary operations on sequences of discrete elements. (Notions in physics like the Ising model do not appear to have had a direct influence.)
The best-known way in which cellular automata were introduced (and which eventually led to their name) was through work by John von Neumann in trying to develop an abstract model of self-reproduction in biology - a topic which had emerged from investigations in cybernetics. Around 1947 - perhaps based on chemical engineering - von Neumann began by thinking about models based on 3D factories described by partial differential equations. Soon he changed to thinking about robotics and imagined perhaps implementing an example using a toy construction set. By analogy to electronic circuit layouts he realized however that 2D should be enough. And following a 1951 suggestion from Stanislaw Ulam (who may have already independently considered the problem) he simplified his model and ended up with a 2D cellular automaton (he apparently hoped later to convert the results back to differential equations). The particular cellular automaton he constructed in 1952-3 had 29 possible colors for each cell, and complicated rules specifically set up to emulate the operations of components of an electronic computer and various mechanical devices. To give a mathematical proof of the possibility of self-reproduction, von Neumann then outlined the construction of a 200,000 cell configuration which would reproduce itself (details were filled in by Arthur Burks in the early 1960s). Von Neumann appears to have believed - presumably in part from seeing the complexity of actual biological organisms and electronic computers - that something like this level of complexity would inevitably be necessary for a system to exhibit sophisticated capabilities such as self-reproduction. In this book I show that this is absolutely not the case, but with the intuition he had from existing mathematics and engineering von Neumann presumably never imagined this.
Two immediate threads emerged from von Neumann’s work. The first, mostly in the 1960s, was increasingly whimsical discussion of building actual self-reproducing automata - often in the form of spacecraft. The second was an attempt to capture more of the essence of self-reproduction by mathematical studies of detailed properties of cellular automata. Over the course of the 1960s constructions were found for progressively simpler cellular automata capable of self-reproduction (see page 1186) and universal computation (see page 1121). Starting in the early 1960s a few rather simple general features of cellular automata thought to be relevant to self-reproduction were noticed - and were studied with increasingly elaborate technical formalism. (An example was the so-called Garden of Eden result that there can be configurations in cellular automata that arise only as initial conditions; see page 963.) There were also various explicit constructions done of cellular automata whose behavior showed particular simple features perhaps relevant to self-reproduction (such as so-called firing squad synchronization, as on page 1039).
By the end of the 1950s it had been noted that cellular automata could be viewed as parallel computers, and particularly in the 1960s a sequence of increasingly detailed and technical theorems - often analogous to ones about Turing machines - were proved about their formal computational capabilities. At the end of the 1960s there then began to be attempts to connect cellular automata to mathematical discussions of dynamical systems - although as discussed below this had in fact already been done a decade earlier, with different terminology. And by the mid-1970s work on cellular automata had mostly become quite esoteric, and interest in it largely waned. (Some work nevertheless continued, particularly in Russia and Japan.) Note that even in computer science various names for cellular automata were used, including tessellation automata, cellular spaces, iterative automata, homogeneous structures and universal spaces.
As mentioned in the main text, there were by the late 1950s already all sorts of general-purpose computers on which simulations of cellular automata would have been easy to perform. But for the most part these computers were used to study traditional much more complicated systems such as partial differential equations. Around 1960, however, there were a couple of simulations related to 2D cellular automata done. Stanislaw Ulam and others used computers at Los Alamos to produce a handful of examples of what they called recursively defined geometrical objects - essentially the results of evolving generalized 2D cellular automata from single black cells (see page 930). Especially after obtaining larger pictures in 1967, Ulam noted that in at least one case fairly simple growth rules generated a complicated pattern, and mentioned that this might be relevant to biology. But perhaps because almost no progress was made on this with traditional mathematical methods, the result was not widely known, and was never pursued. (Ulam tried to construct a 1D analog, but ended up not with a cellular automaton, but instead with the sequences based on numbers discussed on page 910.) Around 1961 Edward Fredkin simulated the 2D analog of rule 90 on a PDP-1 computer, and noted its self-reproduction properties (see page 1186), but was generally more interested in finding simple physics-like features.
Despite the lack of investigation in science, one example of a cellular automaton did enter recreational computing in a major way in the early 1970s. Apparently motivated in part by questions in mathematical logic, and in part by work on "simulation games" by Ulam and others, John Conway in 1968 began doing experiments (mostly by hand, but later on a PDP-7 computer) with a variety of different 2D cellular automaton rules, and by 1970 had come up with a simple set of rules he called "The Game of Life", that exhibit a range of complex behavior (see page 249). Largely through popularization in Scientific American by Martin Gardner, Life became widely known. An immense amount of effort was spent finding special initial conditions that give particular forms of repetitive or other behavior, but virtually no systematic scientific work was done (perhaps in part because even Conway treated the system largely as a recreation), and almost without exception only the very specific rules of Life were ever investigated. (In 1978 as a possible 1D analog of Life easier to implement on early personal computers Jonathan Millen did however briefly consider what turns out to be the code 20 k=2, r=2 totalistic rule from page 283.)
Quite disconnected from all this, even in the 1950s, specific types of 2D and 1D cellular automata were already being used in various electronic devices and special-purpose computers. In fact, when digital image processing began to be done in the mid-1950s (for such applications as optical character recognition and microscopic particle counting) 2D cellular automaton rules were usually what was used to remove noise. And for several decades starting in 1960 a long line of so-called cellular logic systems were built to implement 2D cellular automata, mainly for image processing. Most of the rules used were specifically set up to have simple behavior, but occasionally it was noted as a largely recreational matter that for example patterns of alternating stripes ("custering") could be generated.
In the late 1950s and early 1960s schemes for electronic miniaturization and early integrated circuits were often based on having identical logical elements laid out on lines or grids to form so-called cellular arrays. In the early 1960s there was for a time interest in iterative arrays in which data would be run repeatedly through such systems. But few design principles emerged, and the technology for making chips with more elaborate and less uniform circuits developed rapidly. Ever since the 1960s the idea of making array or parallel computers has nevertheless resurfaced repeatedly, notably in systems like the ILLIAC IV from the 1960s and 1970s, and systolic arrays and various massively parallel computers from the 1980s. Typically the rules imagined for each element of such systems are however immensely more complicated than for any of the simple cellular automata I consider.
From at least the early 1940s, electronic or other digital delay lines or shift registers were a common way to store data such as digits of numbers, and by the late 1940s it had been noted that so-called linear feedback shift registers (see page 976) could generate complicated output sequences. These systems turn out to be essentially 1D additive cellular automata (like rule 90) with a limited number of cells (compare page 259). Extensive algebraic analysis of their behavior was done starting in the mid-1950s, but most of it concentrated on issues like repetition periods, and did not even explicitly uncover nested patterns. (Related analysis of linear recurrences over finite fields had been done in a few cases in the 1800s, and in some detail in the 1930s.) General 1D cellular automata are related to nonlinear feedback shift registers, and some explorations of these - including ones surprisingly close to rule 30 (see page 1093) - were made using special-purpose hardware by Solomon Golomb in 1956-9 for applications in jamming-resistant radio control - though again concentrating on issues like repetition periods. Linear feedback shift registers quickly became widely used in communications applications. Nonlinear feedback shift registers seem to have been used extensively for military cryptography, but despite persistent rumors the details of what was done continue to be secret.
In pure mathematics, infinite sequences of 0’s and 1’s have been considered in various forms since at least the late 1800s. Starting in the 1930s the development of symbolic dynamics (see page 963) led to the investigation of mappings of such sequences to themselves. And by the mid-1950s studies were being made (notably by Gustav Hedlund) of so-called shift-commuting block maps - which turn out to be exactly 1D cellular automata (see page 963). In the 1950s and early 1960s there was work in this area (at least in the U.S.) by a number of distinguished pure mathematicians, but since it was in large part for application to cryptography, much of it was kept secret. And what was published was mostly abstract theorems about features too global to reveal any of the kind of complexity I discuss.
Specific types of cellular automata have also arisen - usually under different names - in a vast range of situations. In the late 1950s and early 1960s what were essentially 1D cellular automata were studied as a way to optimize circuits for arithmetic and other operations. From the 1960s onward simulations of idealized neural networks some× had neurons connected to neighbors on a grid, yielding a 2D cellular automaton. Similarly, various models of active media - particularly heart and other muscles - and reaction-diffusion processes used a discrete grid and discrete excitation states, corresponding to a 2D cellular automaton. (In physics, discrete idealizations of statistical mechanics and dynamic versions of systems like the Ising model were some× close to cellular automata, except for the crucial difference of having randomness built into their underlying rules.) Additive cellular automata such as rule 90 had implicitly arisen in studies of binomial coefficient modulo primes in the 1800s (see page 870), but also appeared in various settings such as the "forests of stunted trees" studied around 1970.
Yet by the late 1970s, despite all these different directions, research on systems equivalent to cellular automata had largely petered out. That this should have happened just around the time when computers were first becoming widely available for exploratory work is ironic. But in a sense it was fortunate, because it allowed me when I started working on cellular automata in 1981 to define the field in a new way (though somewhat to my later regret I chose - in an attempt to recognize history - to use the name "cellular automata" for the systems I was studying). The publication of my first paper on cellular automata in 1983 (see page 881) led to a rapid increase of interest in the field, and over the years since then a steadily increasing number of papers (as indicated by the number of source documents in the Science Citation Index shown below) have been published on cellular automata - almost all following the directions I defined.
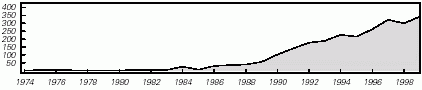
Stephen Wolfram, A New Kind of Science (Wolfram Media, 2002), page 876.
© 2002, Stephen Wolfram, LLC
|
|