SOME HISTORICAL NOTES From: Stephen Wolfram, A New Kind of Science Notes for Chapter 9: Fundamental Physics Section: Elementary Particles Page 1043 History [of elementary particles]. The idea that matter - and light - might be made up of discrete particles was already discussed in antiquity (see page 876). But it was only in the mid-1800s that there started to be real evidence for the existence of some kind of discrete atoms of matter. Yet at the time, the idea of fields was popular, and it was believed that the universe must be filled with a continuous fluid-like ether responsible at least for light and other electromagnetic phenomena. So for example following ideas of William Rankine from 1849 William Thomson (Kelvin) in 1867 suggested that perhaps atoms might be like knotted stable vortex rings in the ether - with different knots corresponding to different chemical elements. But though it initiated the mathematical classification of knots, and now has certain conceptual similarities to what I discuss in this book, the details of this model did not work out - and it had been largely abandoned even before the electron was discovered in 1897. Ernest Rutherford’s work in the 1910s on scattering from atoms introduced the idea of an atomic nucleus, and after the discovery of the neutron in 1932 it became clear that the main constituents of nuclei were protons and neutrons. The positron and the muon were discovered in cosmic rays in the 1930s, followed in the 1940s by a handful of other particles. By the 1960s particle accelerators were finding large numbers of new particles every year. And the hypothesis was then suggested that all these particles might actually be composed of just three more fundamental particles that became known as quarks. An alternative so-called democratic or bootstrap hypothesis was also suggested: that somehow any particle could just be viewed as a composite of all others with the same overall properties - with everything being determined by consistency in the web of interactions between particles, and no particles in a sense being more fundamental than others. But by the early 1970s experiments on so-called deep inelastic scattering had given increasingly direct evidence for point-like constituents inside particles like protons - and by the mid-1970s these were routinely identified with quarks. As soon as the electron was discovered there were questions about its possible size. For if its charge was distributed over a sphere of radius r, this was expected to lead to electrostatic repulsion energy proportional to 1/r. And although it was suggested around 1900 that effects associated with this might account for the mass of the electron, this ran into problems with relativity theory, and it also remained mysterious just what might hold the electron together. (A late suggestion made in 1953 by Hendrik Casimir was that it could be forces associated with zero-point fluctuations in quantum fields - but at least with the simplest setup these turned out to have wrong sign.) The development of quantum theory in the 1920s showed that discrete particles will inevitably exhibit continuous wave-like features in their spatial distribution of probability amplitudes. But traditional quantum mechanics and quantum field theory are both normally formulated with the assumption that the basic particles they describe have zero intrinsic spatial size. Some× nonzero size is taken into account by inserting additional interaction parameters - as done in the 1950s with magnetic moments and form factors of protons and neutrons. But for example in quantum electrodynamics the definite assumption is made that electrons are intrinsically of zero size. Quantum fluctuations make any particle in an interacting field theory effectively be surrounded by virtual particles. Yet not unlike in classical electrodynamics having zero intrinsic size for the electron still immediately suggests that an electron should have infinite self-energy. In the 1930s ideas about avoiding this centered around modifying basic laws of electrodynamics or the structure of spacetime (see page 1031). But the development of renormalization in the 1940s showed that these infinities could in effect just be factored out. And by the 1960s a long series of successes in the predictions of QED had led to the almost universal belief that its assumption of point-like electrons must be correct. It was occasionally suggested that the muon might be some kind of composite object. But experiments seemed to indicate that it was in every way identical to the electron, except in mass. And although no reasonable explanation for its existence was found, it came to be generally assumed by the 1970s that it was just another point-like particle. And indeed - apart from few rare suggestions to the contrary - the same is now assumed throughout mainstream practical particle physics for all of the basic particles that appear in the Standard Model. (Actual experiments based on high-energy scattering and precision magnetic moment measurements have shown only that electrons and muons must have sizes smaller than about hc/(10 TeV) 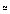10^-20 m - or about 10^-5 × the size of a proton. One can make arguments that composite particles this small should have masses much larger than are observed - but it is easy to find theories that avoid these.) In the 1980s superstring theory introduced the idea that particles might actually be tiny 1D strings - with different types of particles corresponding essentially just to strings in different modes of vibration. Since the 1960s it has been noted in many simplified quantum field theories that there can be a kind of duality in which a soliton or other extended field configuration in one representation becomes what acts like an elementary particle in another representation. And in the late 1990s there were indications that such phenomena could occur in generalized string theories - leading to suggestions of at least an abstract correspondence between for example particles like electrons and gravitational configurations like black holes. Stephen Wolfram, A New Kind of Science (Wolfram Media, 2002), page 1043. © 2002, Stephen Wolfram, LLC