| |
SOME HISTORICAL NOTES

From: Stephen Wolfram, A New Kind of Science
Notes for Chapter 8: Implications for Everyday Systems
Section: Growth of Plants and Animals
Page 1008
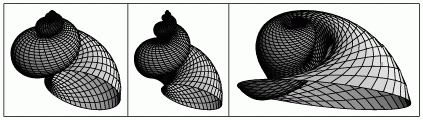
History [of shell models]. Following Aristotle’s notion of gnomon figures that keep the same shape when they grow, equiangular spirals were discussed by René Descartes in 1638, and soon thereafter Christopher Wren noted their relation to shells. A clear mathematical model of shell growth based on equiangular spirals was given by Henry Moseley in 1838, and the model used here is a direct extension of his. Careful studies from the mid-1800s to mid-1900s validated Moseley’s basic model for a wide variety of shells, though an increasing emphasis was placed on shells that showed deviations from the model. In the mid-1960s David Raup used early computer graphics to generate pictures for various ranges of parameters, but perhaps because he considered only specific classes of molluscs there emerged from his work the belief that parameters of shells are greatly constrained - with explanations being proposed based on optimization of such features as strength, relative volume, and stability when falling through water. But as discussed in the main text I strongly suspect that in fact there are no such global constraints, and instead almost all reasonable values of parameters from the simple model used do actually occur in real molluscs. In the past few decades, increasingly complex models for shells have been constructed, typically focusing on fairly specific or unusual cases. Most of these models have far more parameters than the simple one used here, and by varying these parameters it is almost always possible to get forms that probably do not correspond to real shells. And presumably the reason for this is just that such models represent processes that do not occur in the growth of actual molluscs. One widespread issue concerns the orientation of the opening to a shell. The model used here assumes that this opening always stays vertical - which appears to be what happens most often in practice. But following the notion of Frenet frames in differential geometry, it has often come to be supposed that the opening to a shell instead typically lies in a plane perpendicular to the helix traced out by the growth of the shell. This idea, however, leads to twisted shapes like those shown below that occur rarely, if ever, in actual shells. And in fact, despite elaborate efforts of computer graphics it has proved rather difficult with parametrizations based on Frenet frames to produce shells that have a reasonable range of realistic shapes.
Stephen Wolfram, A New Kind of Science (Wolfram Media, 2002), page 1008.
© 2002, Stephen Wolfram, LLC
|
|