Hexagonal array corresponding to flat two-dimensional space — A hexagonal array corresponding to flat two-dimensional space.

consistent with those followed by objects moving under the influence of gravity associated with the given distribution of matter.

For a continuous surface—or in general a continuous space—the idea of curvature is a familiar one in traditional geometry. But if the universe is at an underlying level just a discrete network of nodes then how does curvature work? At some level the answer is that on large scales the discrete network must approximate continuous space.

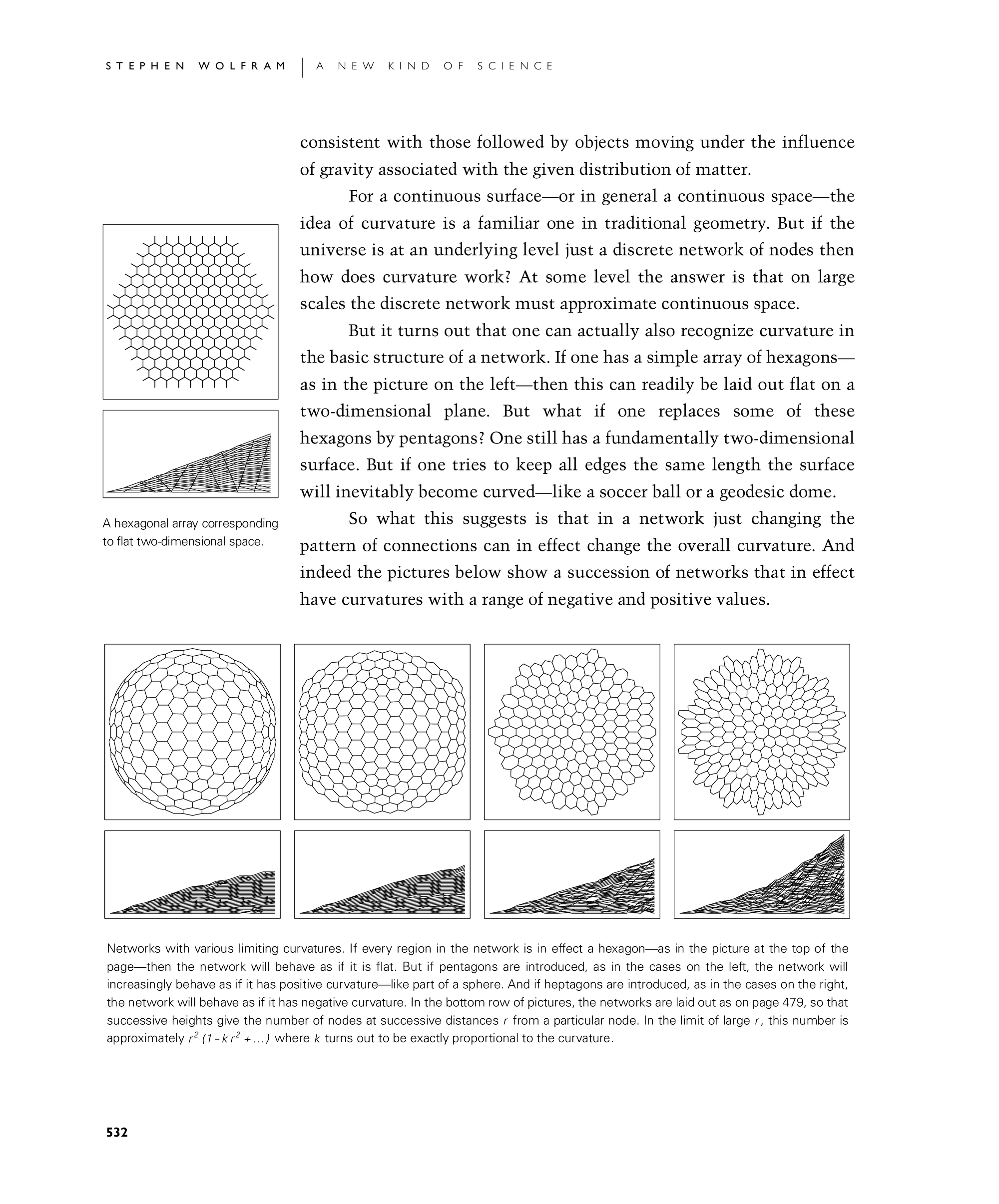
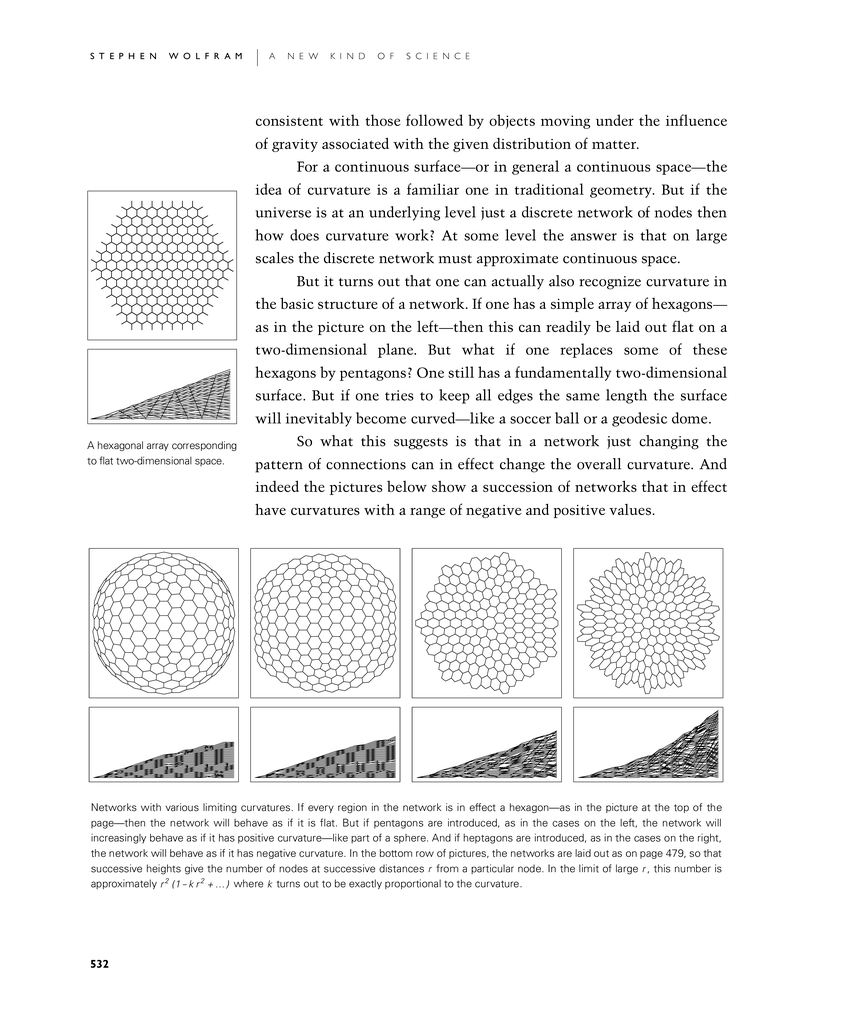
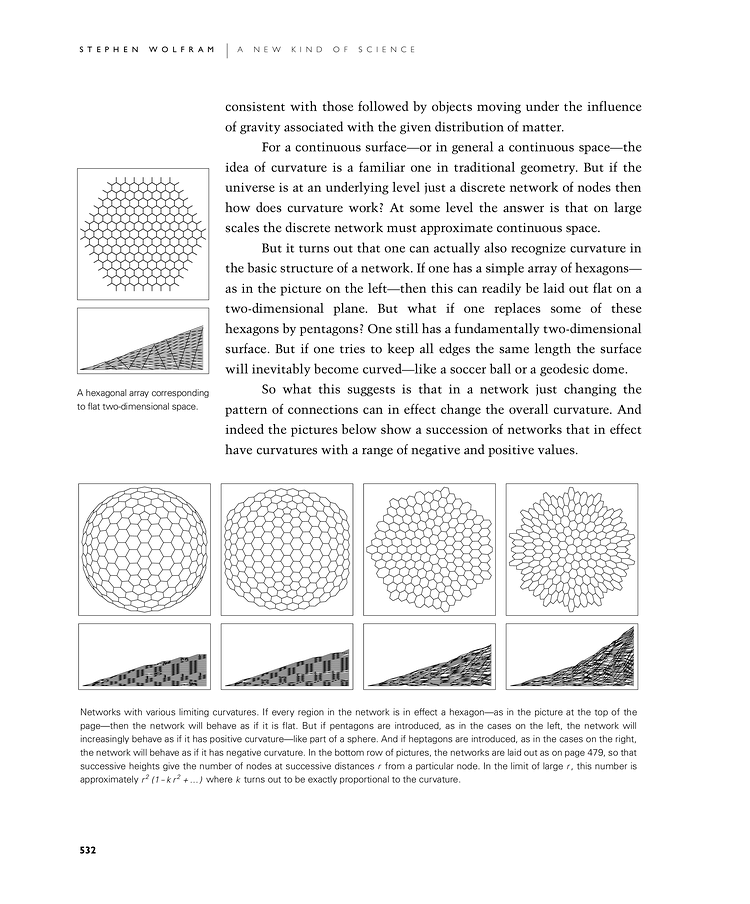
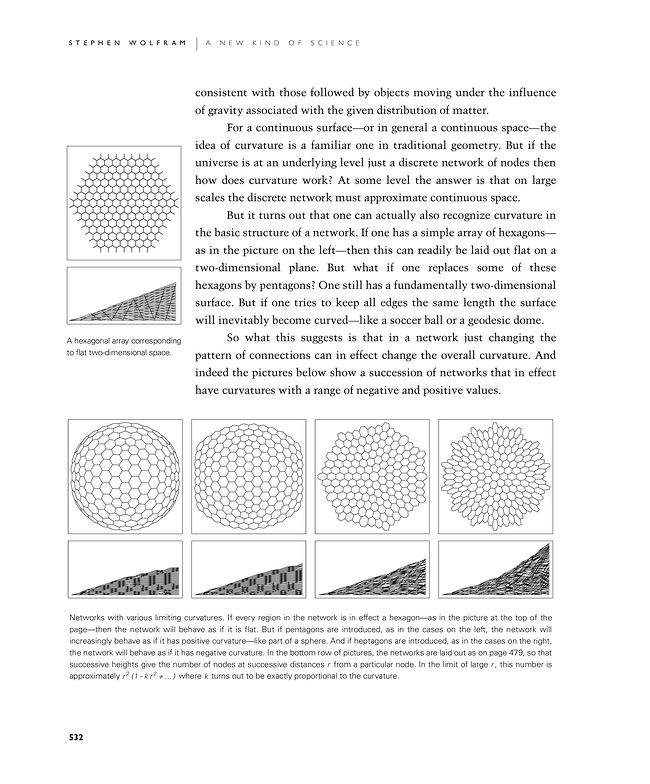
But it turns out that one can actually also recognize curvature in the basic structure of a network. If one has a simple array of hexagons—as in the first picture below—then this can readily be laid out flat on a two-dimensional plane. But what if one replaces some of these hexagons by pentagons? One still has a fundamentally two-dimensional surface. But if one tries to keep all edges the same length the surface will inevitably become curved—like a soccer ball or a geodesic dome.

So what this suggests is that in a network just changing the pattern of connections can in effect change the overall curvature. And indeed the bottom pictures show a succession of networks that in effect have curvatures with a range of negative and positive values.

Networks with various limiting curvatures. If every region in the network is in effect a hexagon—as in the picture at the top of the page—then the network will behave as if it is flat. But if pentagons are introduced, as in the cases on the left, the network will increasingly behave as if it has positive curvature—like part of a sphere. And if heptagons are introduced, as in the cases on the right, the network will behave as if it has negative curvature. In the bottom row of pictures, the networks are laid out as on page 479, so that successive heights give the number of nodes at successive distances r from a particular node. In the limit of large r, this number is approximately r² (1- k r² + …) where k turns out to be exactly proportional to the curvature.