such case, the pattern must repeat itself with a period of at most 2ⁿ steps, where n is the size of the pattern.

In a class 2 system with random initial conditions, a similar thing happens: since different parts of the system do not communicate with each other, they all behave like separate patterns of limited size. And in fact in most class 2 cellular automata these patterns are effectively only a few cells across, so that their repetition periods are necessarily quite short.

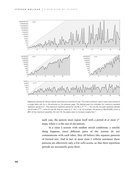
Repetition periods for various cellular automata as a function of size. The initial conditions used in each case consist of a single black cell, as in the pictures on the previous page. The dashed gray line indicates the maximum possible repetition period of 2ⁿ. The maximum repetition period for rule 90 is 2^{(n - 1)/2} - 1. For rule 30, the peak repetition periods are of order 2^{0.63 n}, while for rule 45, they are close to 2ⁿ (for n = 29, for example, the period is 463,347,935, which is 86% of the maximum possible). For rule 110, the peaks seem to increase roughly like n³.