This time the rule specifies that a cell should be black when either its left neighbor or its right neighbor—but not both—were black on the step before. And again this rule is undeniably quite simple. But now the picture shows that the pattern it produces is not so simple.
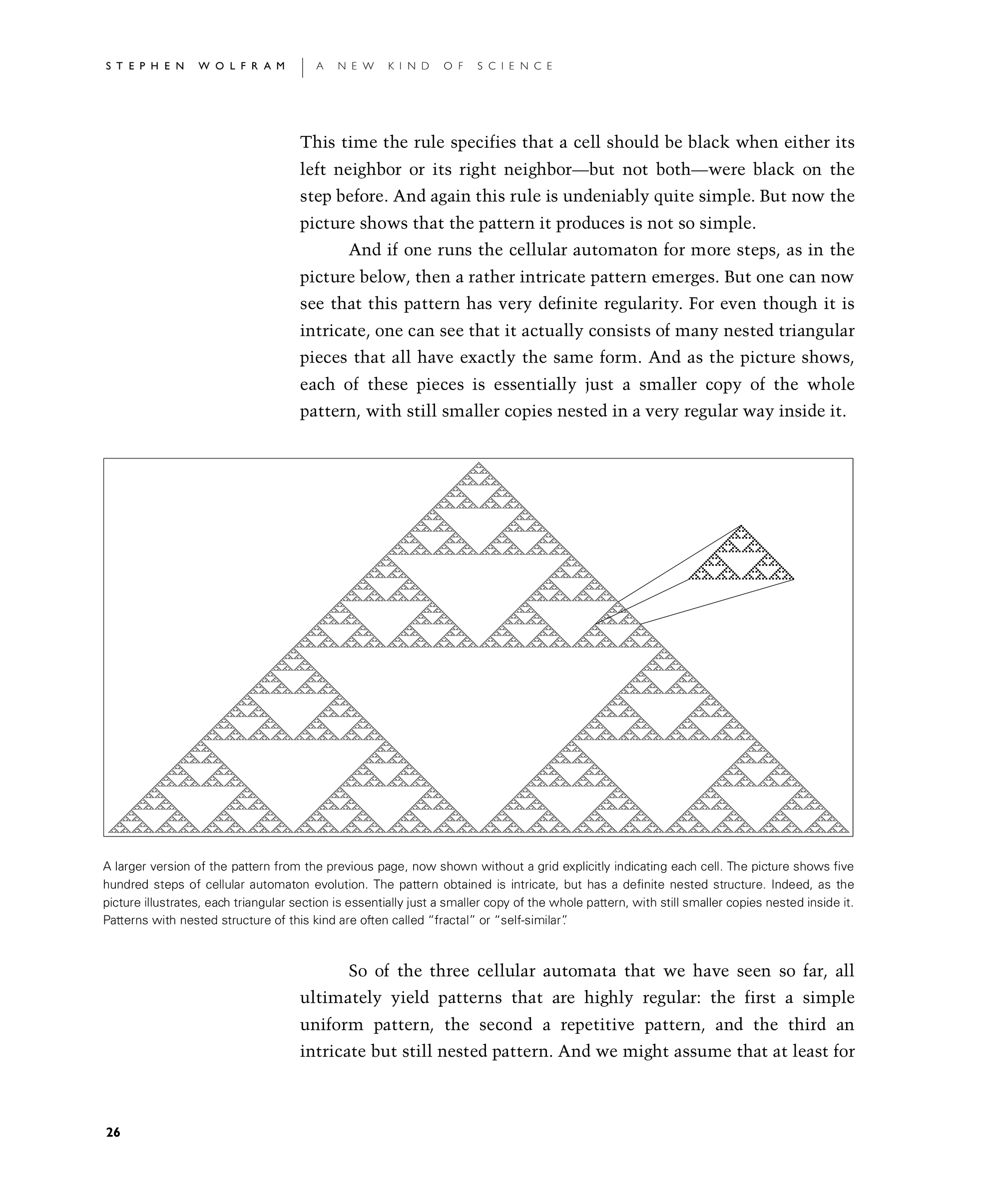
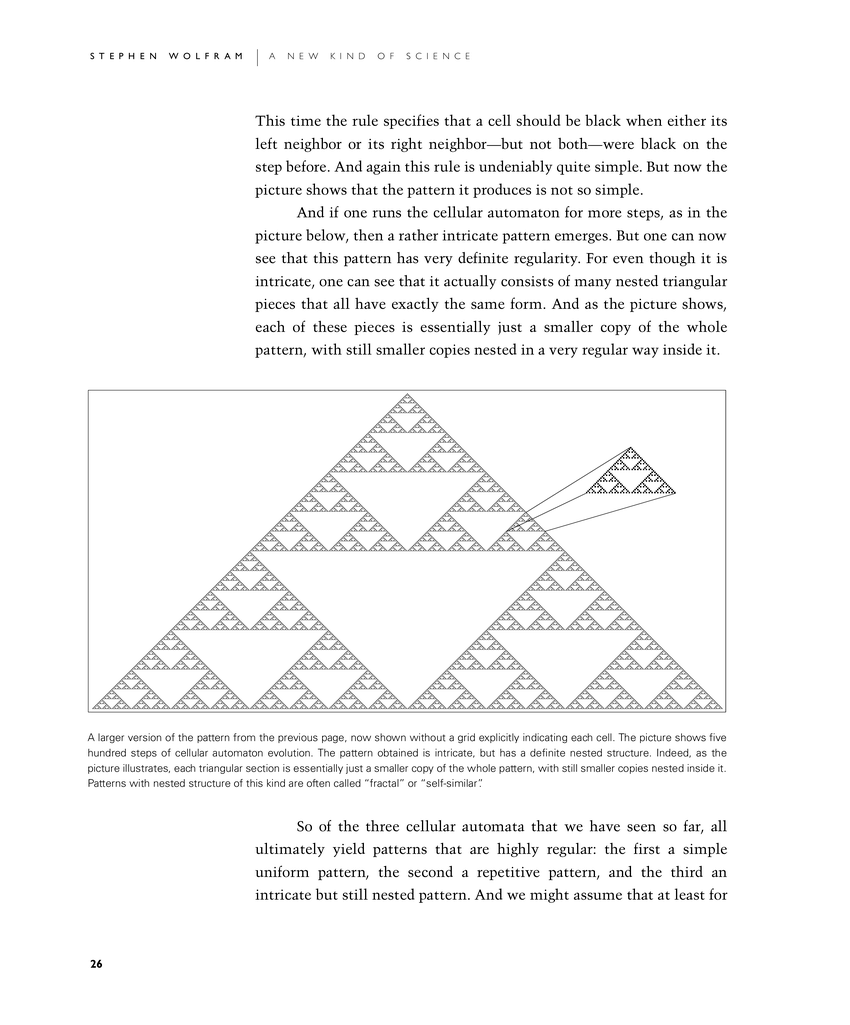
And if one runs the cellular automaton for more steps, as in the picture below, then a rather intricate pattern emerges. But one can now see that this pattern has very definite regularity. For even though it is intricate, one can see that it actually consists of many nested triangular pieces that all have exactly the same form. And as the picture shows, each of these pieces is essentially just a smaller copy of the whole pattern, with still smaller copies nested in a very regular way inside it.
So of the three cellular automata that we have seen so far, all ultimately yield patterns that are highly regular: the first a simple uniform pattern, the second a repetitive pattern, and the third an intricate but still nested pattern. And we might assume that at least for
A larger version of the pattern from the previous page, now shown without a grid explicitly indicating each cell. The picture shows five hundred steps of cellular automaton evolution. The pattern obtained is intricate, but has a definite nested structure. Indeed, as the picture illustrates, each triangular section is essentially just a smaller copy of the whole pattern, with still smaller copies nested inside it. Patterns with nested structure of this kind are often called "fractal" or "self-similar".