making the generated pattern nested. But when α is not a square root the pattern can be more complicated. And if more than two sine functions are involved there no longer seems to be any particular connection to generalized substitution systems or continued fractions.

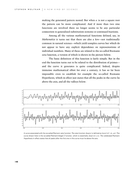
Among all the various mathematical functions defined, say, in Mathematica it turns out that there are also a few—not traditionally common in natural science—which yield complex curves but which do not appear to have any explicit dependence on representations of individual numbers. Many of these are related to the so-called Riemann zeta function, a version of which is shown in the picture below.

The basic definition of this function is fairly simple. But in the end the function turns out to be related to the distribution of primes—and the curve it generates is quite complicated. Indeed, despite immense mathematical effort for over a century, it has so far been impossible even to establish for example the so-called Riemann Hypothesis, which in effect just states that all the peaks in the curve lie above the axis, and all the valleys below.

A curve associated with the so-called Riemann zeta function. The zeta function Zeta[s] is defined as Sum[1/k^s, {k, ∞}]. The curve shown here is the so-called Riemann–Siegel Z function, which is essentially Zeta[1/2 +  t]. The celebrated Riemann Hypothesis in effect states that all peaks after the first one in this curve must lie above the axis.